Medial Surfaces of Polyhedra and Voronoi Diagrams of Lines

The medial axis of a polygon is the set of interior points with more than one closest point on the polygon boundary. The medial axis of an n-gon is a tree consisting of O(n) straight line segments and parabolic arcs. The parabolic arcs are equidistant from a reflex (concave) vertex and an "opposing" edge -- if the polygon is convex, then there are only straight line segments. In the general case, each vertex of the medial axis has degree three, although higher-degree vertices are possible in degenerate cases. The medial axis is a subset of the Voronoi diagram of the edges and vertices of the polygon. (Voronoi edges that meet the reflex vertices are not part of the medial axis.)

The definition generalizes immediately to higher dimensions. In three dimensions, the medial surface of a polyhedron consists of several quadric surface patches -- portions of planes, cones, paraboloids, parabolic cylinders, hyperbolic paraboloids -- sewn together along curve segments of algebraic degree 4. In the general case, each curve bounds three faces, and six faces and four curves meet at each vertex. If the polyhedron is convex, then the medial surface is made up entirely of planar polygonal patches, meeting in straight line segments. Again, the medial surface is a subset of the Voronoi diagram of the vertices, edges and faces of the polyhedron.

What is the worst­case complexity of the medial surface of a polyhedron? It is generally believed that the correct answer is Theta(n²). However, the best known upper bound is O(n^3+c) for any c>0, and even this is not easy to prove! (Any three­dimensional Voronoi diagram is the projection of the lower envelope of several four­dimensional surfaces; the upper bound follows from bounds on the worst­case complexity of lower envelopes by Micha Sharir and others.)

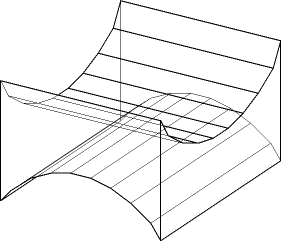
It is quite easy to construct a polyhedron whose medial surface has Omega(n²) faces. For example, we can carve out two shallow cylindrical "trenches", each with n/2 facets, from the top and bottom of a cube, in perpendicular directions. (The depth of the trenches is exaggerated in the figure.)

More surprisingly, a single pair of polyhedron facets can induce Omega(n²) faces in the medial surface, as shown by the following construction, appropriately dubbed the "iron maiden pizza box" by Tim Culver. Start with a rectangular box with height 1, width n, and depth n, resting on the xy­plane and aligned with the coordinate axes. Add O(n) extremely thin horizontal spikes pointing into and almost all the way across the box, half parallel to the x­axis at z=2/5 and half parallel to the y­axis at z=3/5, with successive spikes in each family at distance 2. (If we like, we can eliminate the multiply­connected and parallel facets by triangulating the facets and perturbing the vertices.) The top and bottom facets of the box induce a quadratic number of medial surface features, all in the plane z=1/2.

This construction shows a direct connection with another open problem. What is the worst­case complexity of the Voronoi diagram of a set of lines in 3­space? Again, the best known bounds are O(n^3+c) and Omega(n²). (It has been known for decades that the Voronoi diagram of a set of points in 3­space has only quadratic complexity in the worst case.) For any set L of lines in 3­space, we can construct a simply­connected polyhedron whose medial surface approximates the Voronoi diagram of L arbitrarily closely -- simply replace each line in L by a thin spike poking into an extremely large cube. So there's no hope of improving the complexity bounds for medial surfaces without first understanding the Voronoi diagram of lines.

An offset surface for a polyhedron is the set of points at a given distance r from its boundary, or equivalently, the boundary of the Minkowski sum of the polyhedron and a ball of radius r. What is the worst­case complexity of an offset surface of a polyhedron? When r=0, the offset surface is the original polyhedron; as we increase r, the vertices and edges of the offset surface trace out the edges and faces of the medial axis. Although offset surfaces have lower complexity than medial surfaces, the best known upper bound on their worst­case complexity is still O(n^3+c). Offset surfaces can have quadratic complexity (see the examples above).

Pankaj Agarwal and Micha Sharir have recently shown that the offset surface of any polyhedron with n features, or in fact of any collection of n points, lines, line segments, and triangles, has at most O(n^5/2+c) vertices, an improvement of roughly n^1/2 over the previously best bound. So far at least, their proof does not extend to medial surfaces. [A preliminary version of their results, with a weaker O(n^8/3+c) bound, and only for lines and line segments, will appear at SODA 99.]

Better answers are known for some of these questions in non­Euclidean metrics. Boris Aronov and Micha Sharir showed that in any polyhedral metric, offset surfaces of polyhedra have complexity between Omega(n²alpha(n)) and O(n²log n). Paul Chew, Klara Kedem, Micha Sharir (again!), Boaz Tagansky, and Emo Welzl showed that the Voronoi diagram of lines in a polyhedral metric has complexity O(n²log n alpha(n)). (Here, alpha(n) is the inverse Ackermann function.) I don't know if these results have been extended to medial surfaces.

The complexity of straight skeletons in three dimensions and the mitered offset surfaces that define them is also open. Once again, the best known lower bounds are quadratic, while the best known upper bounds are cubic.

Of course, we can go to four or even higher dimensions and ask the same questions. Boris Aronov has a construction of n lines in d­dimensional space whose Euclidean Voronoi diagram has complexity Omega(n^d-1). The best known upper bound is O(n^d+c).