There are several fast algorithms to generate polygons from other useful (nonuniform) probability distributions. Many of these implemented in the RPG software package by Thomas Auer and Martin Held.
Auer and Held's paper also describes efficient algorithms to generate
starshaped polygons uniformly at random in O(n4) time.
Chong Zhu and his coauthors describe an lineartime algorithm to uniformly generate
monotone polygons. Both papers consider a Markov chain heuristic for genreating
simple polygons that starts with an arbitrary simple polygon an performs random "2OPT
moves" -- delete a pair of edges and reconnect the two resulting pieces the only other
possible way, but backtrack if you get something nonsimple. Unfortunately, this heuristic
leads to a nonuniform distibution of polygons in the limit.
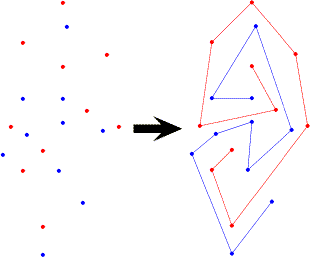
A more or less equivalent question is How quickly can we count all simple polygons with a given set of vertices? Of course, there is an easy exponential time algorithm -- try all (n-1)!/2 possibilities -- but no polynomialtime algorithm is known. It is also not known whether the problem is #Phard. Hiedi Burgiel and Michelle Raymond have written an applet to count simple ngons.
When P is in convex position, SP(P) contains only the convex hull of P, but if the points are in nonconvex position, SP(P) could be exponentially large. Let sp(n) denote the maximum size of SP(P) over all npoint sets P. How big is sp(n)? For all n, which npoint sets define the largest number of simple polygons? Auer and Held prove an O(n4) upper bound on the number of starshaped polygons with a given set of n vertices. The following simple construction of Chirstian Sohler implies a matching lower bound: put n-2 points on the unit parabola y=x2, half on either side of the x-axis, and then add two points far below and to either side of the parabola.
The corresponding questions about other simple geometric objects such as triangulations, simple polygonal paths, and simple spanning trees are also open. Perhaps triangulations have received the most study -- Raimund Seidel proved a lower bound of 23n-Omega(log n), and Markus Denny and Christian Sohler proved an upper bound of 28.2n+O(log n). The problems of counting (and therefore uniformly generating) spanning trees of graphs are wellstudied, but as far as I know, none of those results apply to simple spanning trees of points in the plane. It's not clear to me whether the added restriction makes the problem easier or harder.
The following question may be related. Given two sets of points in the plane, how quickly can we compute a pair of disjoint simple polygons/paths, or report that no such pair exists? As far as I know, this problem has never been studied. I suspect it is NPhard. John Hershberger and I recently developed an algorithm that finds a pair of disjoint simple spanning trees in O(n log n) time, or a short proof that no such trees exist.
Obviously we can generalize the problem to higher dimensions. Given a set of points in 3space, how quickly can we generate a random simple polyhedron? A random tetrahedralization? A random unknotted polygon? Jock Snoeyink has asked the following question: How many triangulated surfaces (say, homoeomorphic to a disk) can n points in 3space determine? Specifically, can it be more than n!, or is it always less? Given two sets of points in 3space, how quickly can we determine whether they are the vertices of two unlinked polygons?
 Open Problems -
Jeff Erickson
(jeffe@cs.uiuc.edu)
09 Apr 1999
Open Problems -
Jeff Erickson
(jeffe@cs.uiuc.edu)
09 Apr 1999