Does every convex polytope have a simple unfolding? An unfolding is simple if it does not intersect itself. This is not a trivial question! There are many examples of polytopes, including some tetrahedra, that have nonsimple unfoldings.
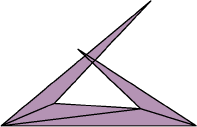
A nonsimple unfolding of a tetrahedron.
(image stolen from Komei Fukuda's
"Strange Unfoldings of Convex Polytopes")
Günther Rote recently constructed a family of polytopes whose minimum-perimeter unfoldings, constructed by cutting along the minimum spanning tree of the polytope's edge graph, are nonsimple. An example is illustrated below. This disproved a conjecture of Komei Fukuda. Fukuda also conjectured that the unfolding obtained by cutting along the shortest-path tree is simple, but apparently this conjecture was disproved by Wolfram Schlickenrieder.
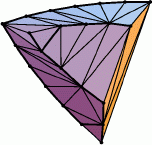
One of Rote's polytopes and its nonsimple minimum-perimeter unfolding.
(images stolen from Komei Fukuda's
"Strange Unfoldings of Convex Polytopes")
We can also describe an unfolding as a spanning tree of the edge graph of the dual (or polar) polytope, where each edge specifies a pair of adjacent faces of the original (primal) polytope. The spanning tree specifies which pairs of faces are not cut apart. Does the minimum spanning tree of the dual edge graph always describe a simple unfolding? Of course, for this question to make sense, we first have to specify how each dual edge is weighted; the dihedral angle at the corresponding primal edge (or some simple function thereof) seems like a promising choice.
Despite the openness of the unfolding problem, Makoto Namiki and Komei Fukuda have written a Mathematica package that tries to find a simple unfolding for a given convex polytope. The package was used to produce most of the images on this page. Another program by Mike Eisenberg and Ann Nishioka called HyperGami includes code to unfold even some nonconvex polytopes. (See this article in American Scientist.) Neither program has ever failed (yet).
If the definition of unfolding is loosened to allow cuts through faces of the polytope, then the "star unfolding" defined by Pankaj Agarwal, Boris Aronov, Joe O'Rourke, and Catherine Schevon is always simple. The star unfolding is defined by cutting along geodesic paths from one vertex to all the other vertices. (This may provide some intuitive evidence for Fukuda's second conjecture.)
Does every convex polytope have an unambiguous unfolding? An unfolding is unambiguous if it cannot be refolded into more than one convex polytope. If we forget the creases when we unfold the polytope, then the answer is no. In fact, the Roman cross unfolding of the cube can be refolded into polytopes with four, five, and eight faces by introducing different crease patterns; see below.
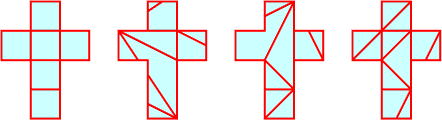
Four ways to refold a cube.
(image stolen from David
Eppstein's "Geometry
Junkyard")
(In their paper "When Can a Polygon Fold to a Polytope?", Anna Lubiw and Joe O'Rourke present an algorithm that finds, at least in principle, all the ways to fold a given simple polygon into a polytope. Their results leave two problems open. First, Lubiw and O'Rourke consider only foldings that glue entire edges together. Relaxing this edge-gluing condition could result in even more polytopes, but no algorithm is known to find them all. More importantly, Lubiw and O'Rourke's algorithm only finds an edge matching describing which pairs of edges to glue together. No algorithm is known to construct the actual polytope, or even the crease pattern, from an edge matching. The figure above was produced by hand by David Eppstein from a list of edge matchings found by Lubiw and O'Rourke's algorithm. Several similar open problems are described on a separate webpage.)
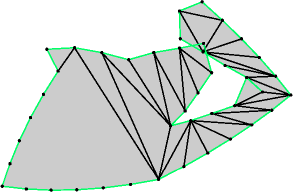
If creases are always included in any unfolding, the ambiguous unfolding question is still open. There are (creased) unfoldings that can be refolded into more than one polytope. Tomomi Matsui has constructed a 6-facet, 5-vertex unfolding that can be refolded into two polytopes, each a mirror image of the other. Günther Rote recently constructed an unfolding that can be refolded into two combinatorially distinct polytopes. According to Croft, Falconer, and Guy, examples of this phenomenon were already known in 1991; although they do not provide references, the examples were probably constructed by G. C. Shephard.
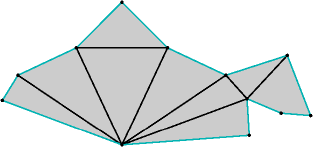
Rote's combinatorially ambiguous unfolding.
(image stolen from Komei Fukuda's
"Strange Unfoldings of Convex Polytopes")
For more details, see Komei Fukuda's Web page "Strange Unfoldings of Convex Polytopes". Catherine Schevon discusses the history of the simple unfolding problem and some early results in this article from David Eppstein's Geometry in Action. Similar results and open problems are described in this page from David's Geometry Junkyard. The simple unfolding problem appears as Problem B21 (pages 73-75) in the fascinating book Unsolved Problems in Geometry by Hallard Croft, Kenneth Falconer, and Richard Guy (Springer-Verlag, 1991).
 Open Problems -
Jeff Erickson
(jeffe@cs.uiuc.edu)
28 May 1999
Open Problems -
Jeff Erickson
(jeffe@cs.uiuc.edu)
28 May 1999