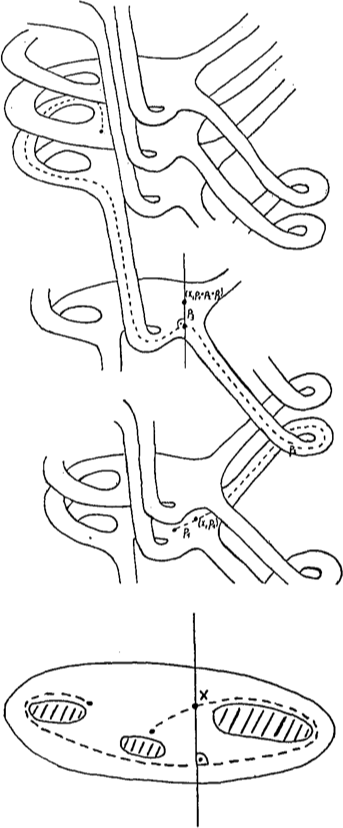
A path in a planar region and a lift to the universal cover.
From Gao et al. [SOCG 1998]
Computational topology is an emerging field of study at the intersection of mathematics and computer science, devoted to the study of efficient algorithms for topological problems, especially those that arise in other areas of computing. Although algorithmic techniques have been ubiquitous in topology since its inception more than a century ago, the efficiency of topological algorithms and their applicability to other computing domains are relatively recent areas of study. Results in computational topology combine classical mathematical techniques from combinatorial, geometric, and algebraic topology with more recent algorithmic tools from data structure design and computational geometry. These results have found applications in many different areas of computer science.
This course will be a broad introduction to computational topology; the precise topics covered will depend on the skills and interests of the course participants. Potential mathematical topics include the topology of cell complexes, topological graph theory, homotopy, covering spaces, simplicial homology, persistent homology, discrete Morse theory, discrete differential geometry, and normal surface theory. Potential computing topics include algorithms for computing topological invariants, graphics and geometry processing, mesh generation, curve and surface reconstruction, VLSI routing, motion planning, manifold learning, clustering, image processing, and combinatorial optimization.
Students in all areas of computer science, mathematics, and related disciplines are welcome. CS 573 and/or Math 525 are recommended as prerequisites, but not required; necessary background material will be introduced as needed.