One-Dimensional Computational Topology
The most recent offering of this class is available
here.

Paul Klee,
Zur Gruppe geschlungen [Entwined in a Group] (1930)
Paul Klee Zentrum, Bern
Announcements
- December 1
- The makeup lectures will be held from 12 to 1:15 in 3401 Siebel, both today and next Friday.
- November 16
- I will give makeup lectures on the next two Fridays after Thanksgiving break. Please fill out this Doodle poll to let me know when you're available.
- November 10
- An archive of all submitted project proposals is available. Check your email for the required login credentials.
- November 6
- The twice-weekly lecture videos (~1Mb each) have put my web site over quota (~20Mb). I'm looking for alternate storage space, but meanwhile, posting of new lecture videos will be delayed.
- November 1
- Project proposals are due next Friday, November 10. Please submit your proposals on Gradescope. I will present an overview/summary of all submitted proposals on Tuesday, November 14.
- October 9
- Homework 3 is available.
- September 20
- Homework 2 is available.
- September 15
- Thanks to everyone who filled out the Doodle poll. My regular office hours will be Fridays 4–5, starting tomorrow (but not next Friday, because I will be on a plane).
Please sign up on Gradescope so that you can submit homework solutions. The self-enrollment code is MRWX3N. You can sign up using any name and email address you like, but please use a consistent identity in all homework submissions. If you are using anything other than your real name and illinois.edu email address, please fill out this form so I know who you are.
- September 8
- I am holding office hours next Monday, September 11, 3-4pm (not Friday as I announced in class) outside 3304 Siebel. Please fill out this Doodle poll to help me choose a time for regular weekly office hours.
- September 7
- Class is canceled on September 19 and 21, because I will be out of the country. I will schedule makeup lectures later in the semester.
- September 5
- Homework 1 is available. Stay tuned for Gradescope submission instructions.
- August 31
- Registration is now open to everyone. If you are still unable to register for any reason, please let me know.
- August 29
- Please also fill out this form to tell me about your background and interests. This will help be tune both the specific content and the level of detail/difficulty of the class. Thanks!
About this class
This course will be an introduction to my favorite facet of computational topology: Algorithms for curves and graphs embedded in the plane or other surfaces. Algorithmic questions about curves have been a driving force in topology since its inception more than a century ago. Planar and near-planar graphs have long been fertile ground for algorithms research, both because they naturally model many classes of networks that arise in practice, and because they admit simpler and faster algorithms than more general graphs. There is a rich interplay between these two domains, drawing on a common pool of techniques from geometry, topology, and combinatorics. Potential topics include topological graph theory; homotopy, homology, and other topological invariants; specialized algorithms for shortest paths, maximum flows, and minimum cuts; efficient approximation schemes for NP-hard problems; and applications in VLSI design, computer graphics, computer vision, motion planning, geographic information systems, and other areas of computing. Specific topics will depend on the interest and expertise of the students.
Students in all areas of computer science, mathematics, and related disciplines are welcome. CS 473 and/or Math 525 are recommended as prerequisites, but not required; necessary background material will be introduced as needed. Undergraduates interested in taking this course can get a registration override at the first lecture.
Historical Gallery

Nonagonus secundi ordinis. Thomas Bradwardine,
Geometria speculativa (c.1320)
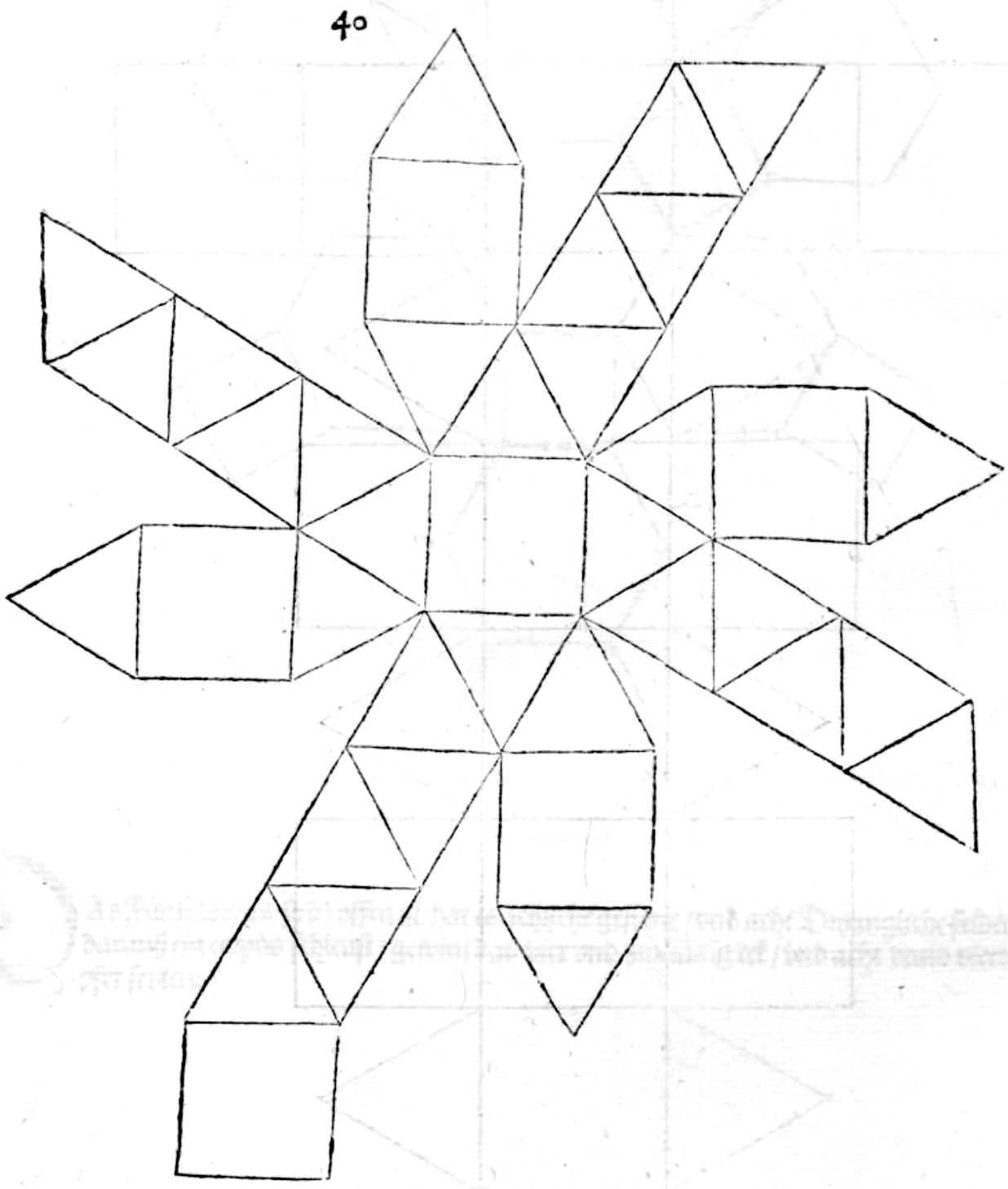
An unfolding of a snub cube. Albrecht Dürer,
Underweysung der messung (1520)
Computing the area of a non-convex polygon. Albrecht Meister,
Generalia de genesi figurarum planarum et inde pendentibus earum affectionibus (1770)
A simple closed curve. Bernard Bolzano,
Die drey Probleme der Rectification, der Complanation und der Cubirung (1817)
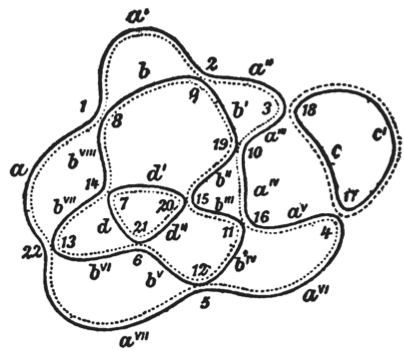
Decomposing a non-simple curve into simple curves. Carl Friedrich Gauß,
Zur Geometria situs (Nachlass) (c.1830)
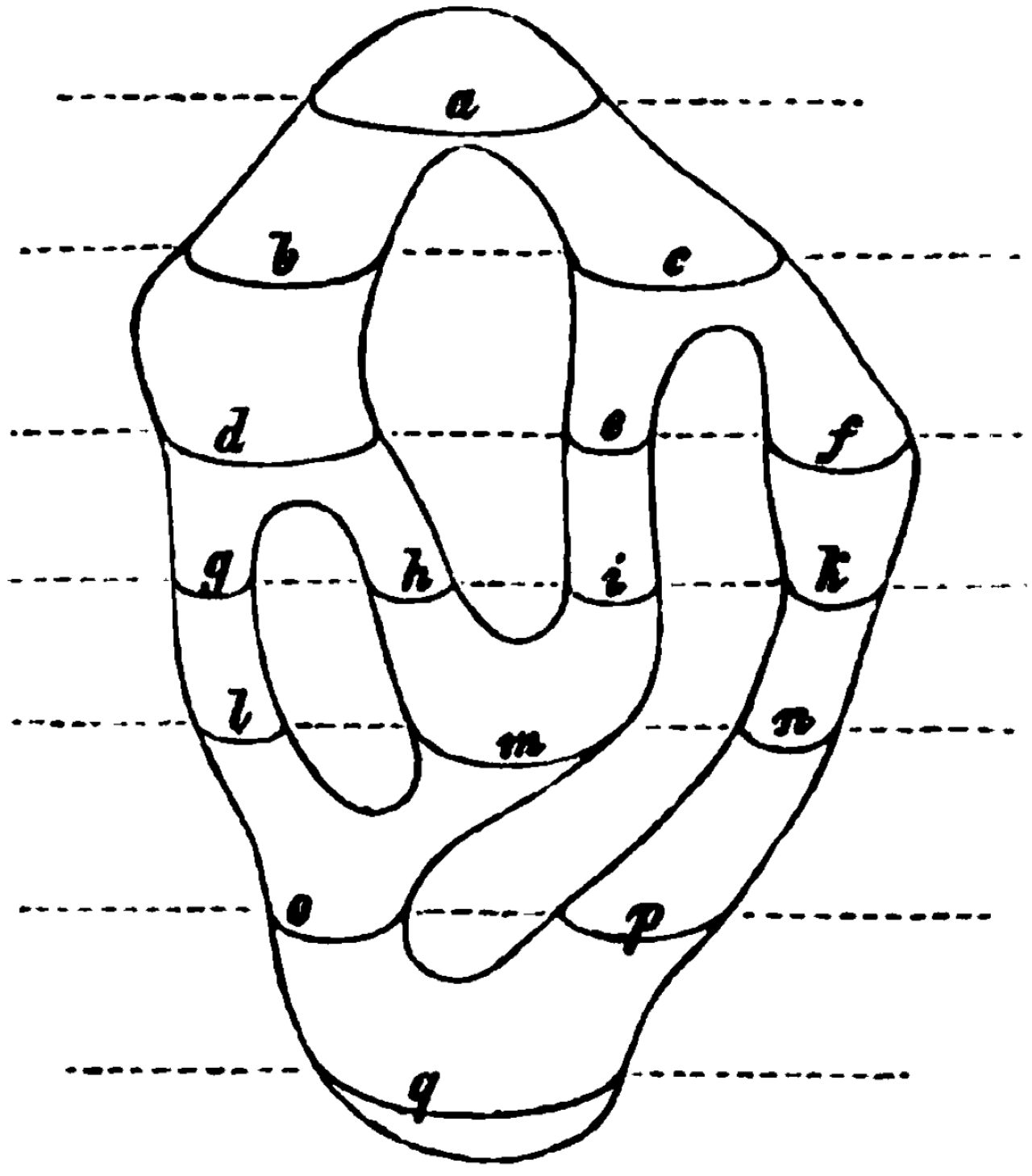
Proving that every convex(!) polygon can be triangulated. Carl Friedrich Gauß,
Zur Geometria situs (Nachlass) (c.1830)

A pants decomposition. Johann Benedict Listing,
Census Räumlicher Complexe (1862)
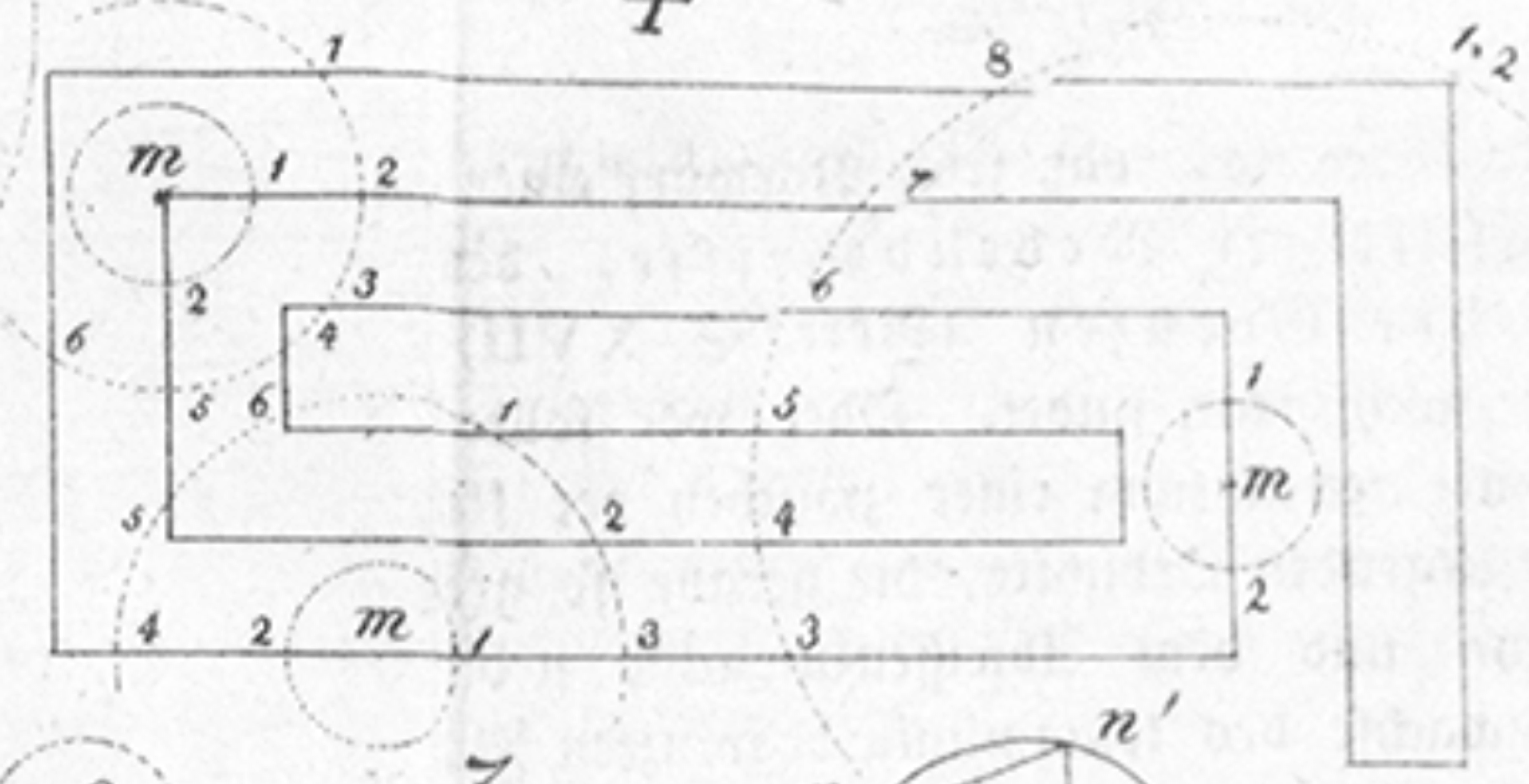
Cutting a surface at non-critical heights. August Möbius,
Theorie dr elementaren Verwandtschaft (1863)
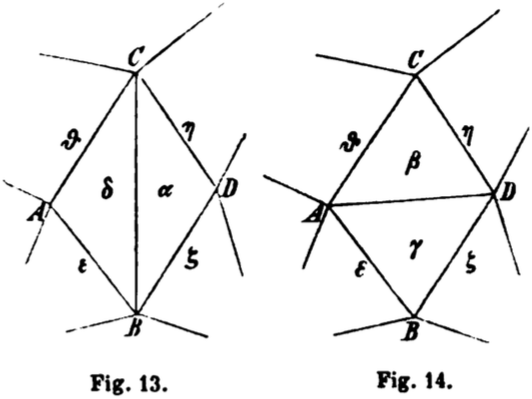
Flipping an edge in a triangulation. August Möbius,
Ueber die Bestimmung des Inhalts eines Polyëders (1865)
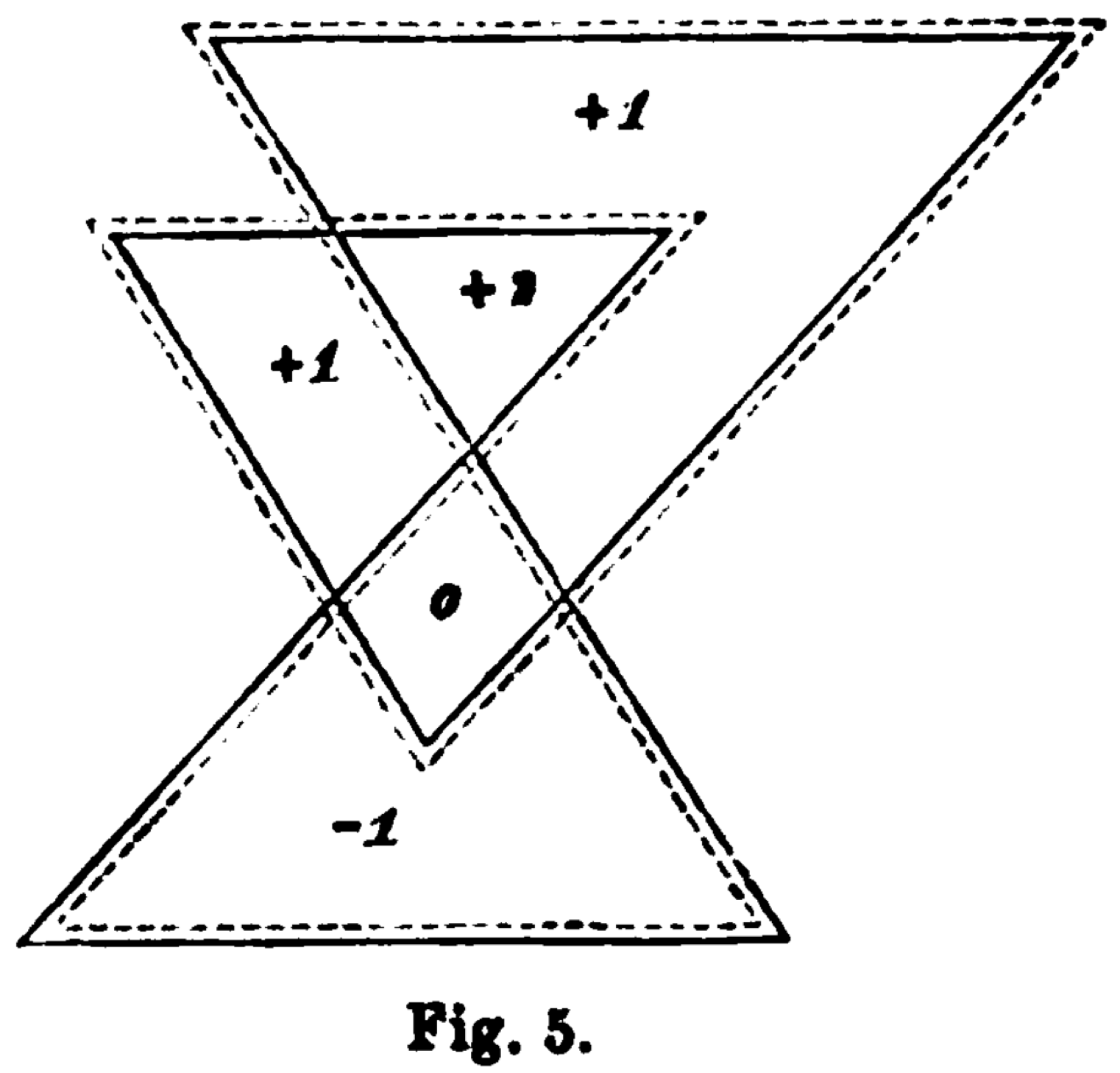
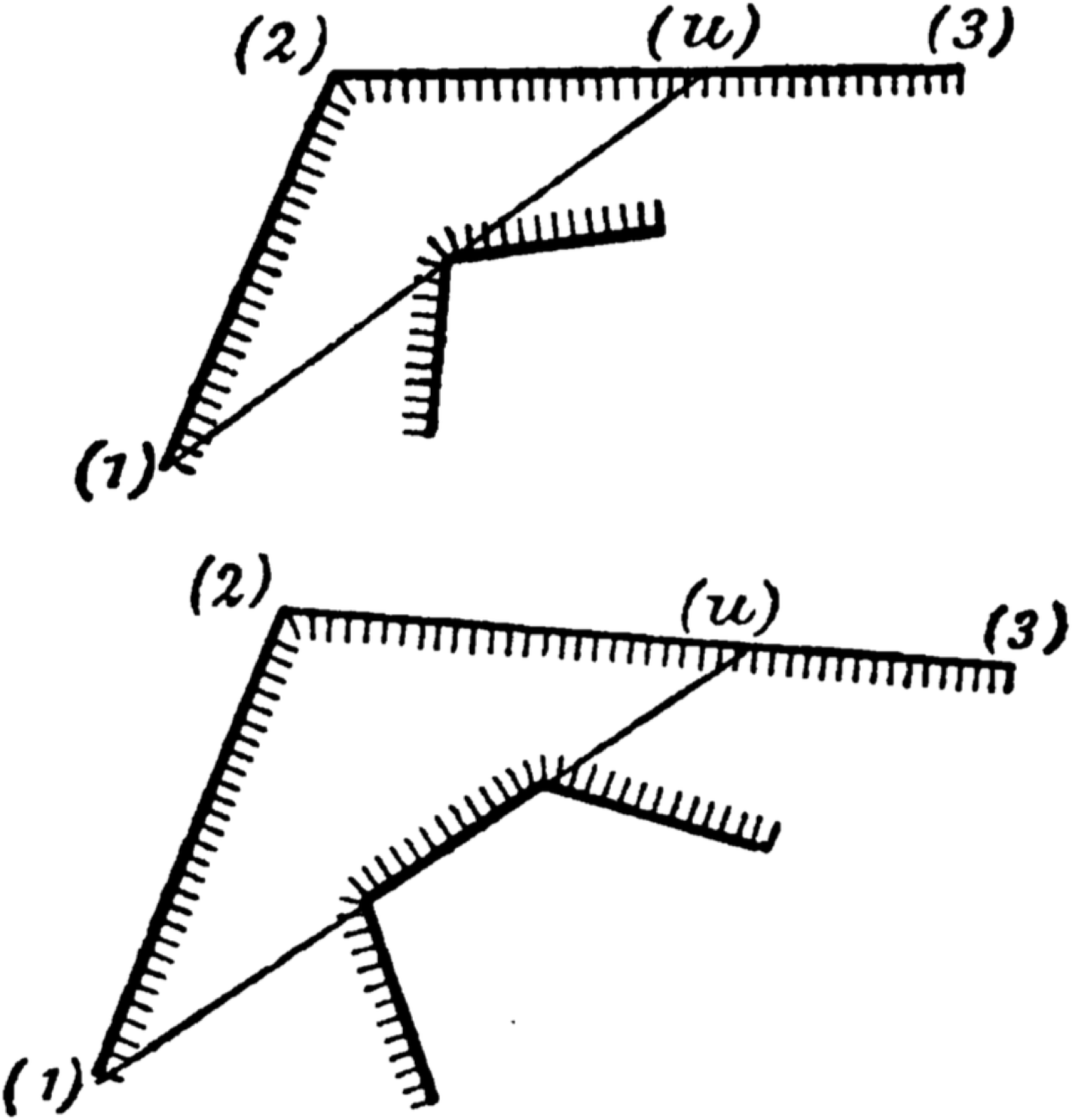
"Alexander" numbering of a nonsimple polygon. August Möbius,
Ueber die Bestimmung des Inhalts eines Polyëders (1865)
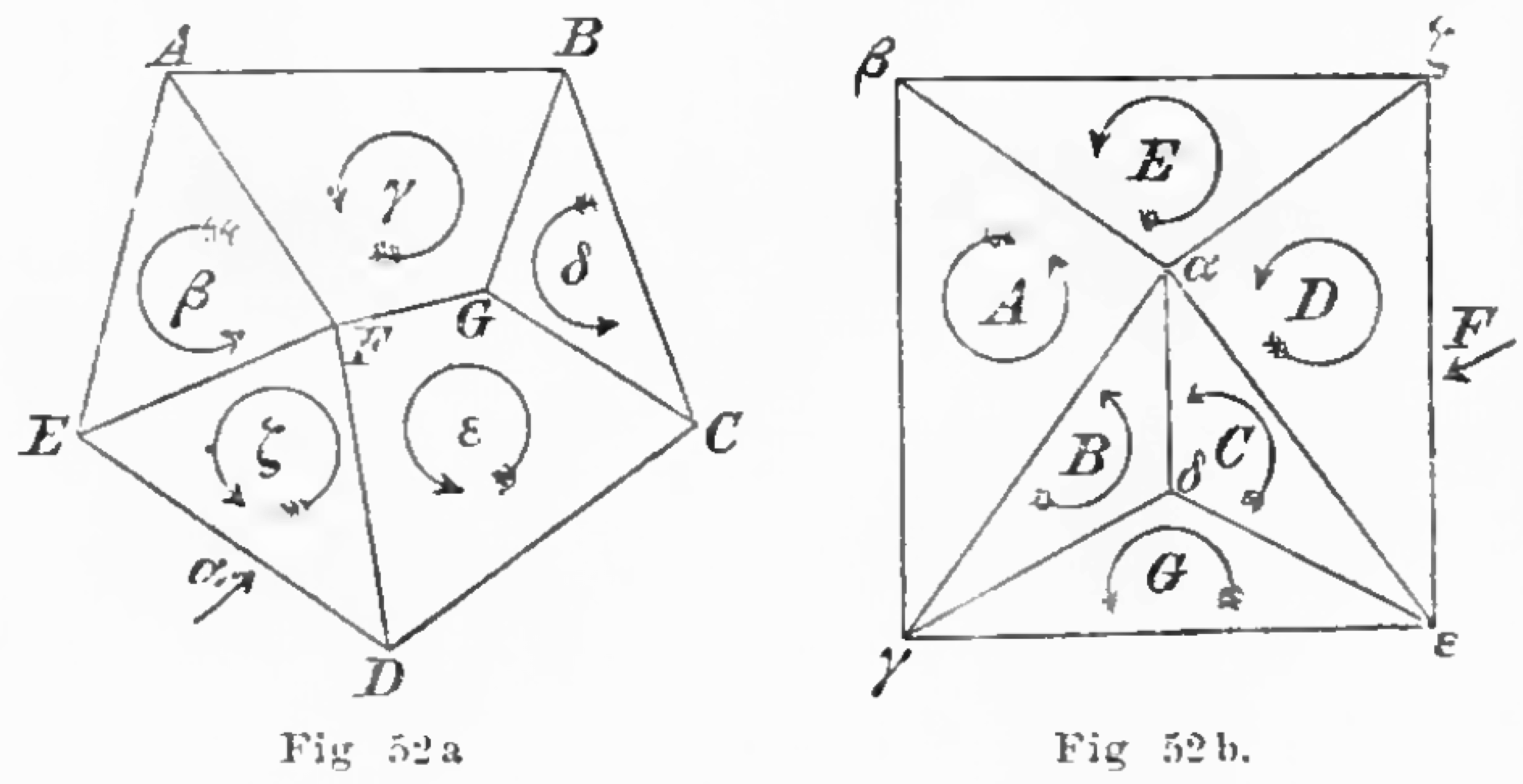
A planar map and its dual, specified by the same rotation system. Max Brückner,
Vielecke und Vielflache: Theorie und Geschichte (1900)

Paul Klee,
Pedagocial Sketchbook (1925), English translation by Sybil Moholy-Nagy (1953)
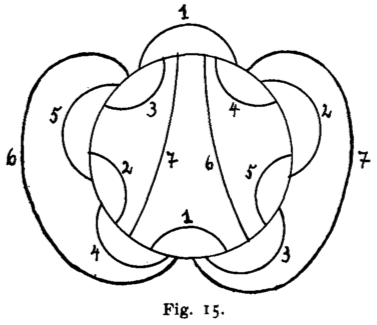
The "tree-onion figure" of a planar map. Max Dehn,
Über kombinatorische Topologie (1936)

Piet Hein's inspirations for the game "Polygon", now known as "Hex". Piet Hein, "Vil de lære Polygon?",
Politiker (December 26, 1942)
Other computational topology classes
The selection of topics in this class is necessarily limited by the finiteness of a single semester and by my own interests and expertise. Important topics in computational topology that I will not cover this semester, except perhaps briefly in passing, include automatic groups, knot theory, 3-manifolds, cell complexes (simplicial, cubical, Delta, CW, simplicial sets), discrete Morse theory, normal surface theory, configuration spaces, dynamical systems, persistent homology and its generalizations, surface reconstruction, manifold learning, topological data analysis, embedding obstructions, higher-order homotopy, discrete differential geometry, fixed-point theorems, applied Hodge theory, algebraic complexity, evasiveness of graph properties, impossibility results in distributed computing, and topological quantum computing. The full diversity of techniques, results, applications, and even definitions of computational topology could easily fill a dozen courses.
Here is an incomplete list of other recent courses in computational topology with publicly available course materials (beyond just a syllabus). Please let me know if you'd like to add your course!
- Henry Adams, Universidad de Costa Rica (Summer 2017)
- Éric Colin de Verdière and Vincent Pilaud, ENS Paris (2016–17) — course notes 1 and course notes 2
- Keenan Crane, CMU (Spring 2016) — course materials
- Isabel Darcy, University of Iowa (Fall 2013)
- Erik Demaine, Shay Mozes, Christian Sommer, and Siamak Tazari, MIT (Fall 2011)
- Tamal Dey, Ohio State (Fall 2013)
- Spike Hughes, Brown University (Spring 2015)
- Misha Kazhdan, Johns Hopkins (Fall 2009)
- Philip Klein, Brown University (Spring 2017) — book draft
- Bala Krishnamoorthy, Washington State University (Spring 2016)
- Francis Lazarus and Arnaud de Mesmay, Université de Grenoble, ENS Lyon (Fall 2016)
- Shay Mozes, IDC Herzliya (Fall 2015)
- Steve Oudot, École polytechnique (2017–18)
- Michael Robinson, American University (Spring 2016)
- Yuan Yao, Stanford University (Spring 2016)