CS 598 JGE: Advanced Data Structures (Fall 2015)

❖ Announcements ❖ Schedule ❖ Projects ❖

❖ Pointers ❖ Tables ❖ Bits ❖ Time ❖ Big Data ❖ Related Topics ❖

Lecture notes are available for the first few lecture topics, but I don't plan to write notes for the rest of the semester.

Key references for each lecture are highlighted. Other references contain related material—historical developments, applications, later improvements and extensions, and the like—which I may only mention briefly (or not at all) in class. Some key sources are cited multiple times. *Starred authors were students when the work was written. These reference lists are out of date, but I will do my best to update them as the semester progresses. Eventually I hope to post a bibtex file that includes everything listed here; stay tuned!

All future lecture topics are subject to change! This schedule mostly mirrors the sequence of topics I covered in Spring 2011. Several relevant topics that I didn't have time to cover are listed after the main schedule; I might cover some of these topics this semester.

I am traveling Oct 15–17, Nov 11, and Dec 2. I hope to schedule makeup lectures outside the normal class meeting time. If scheduling proves prohibitive, I will try to arrange for guest lecturers instead.

Fun with Pointers

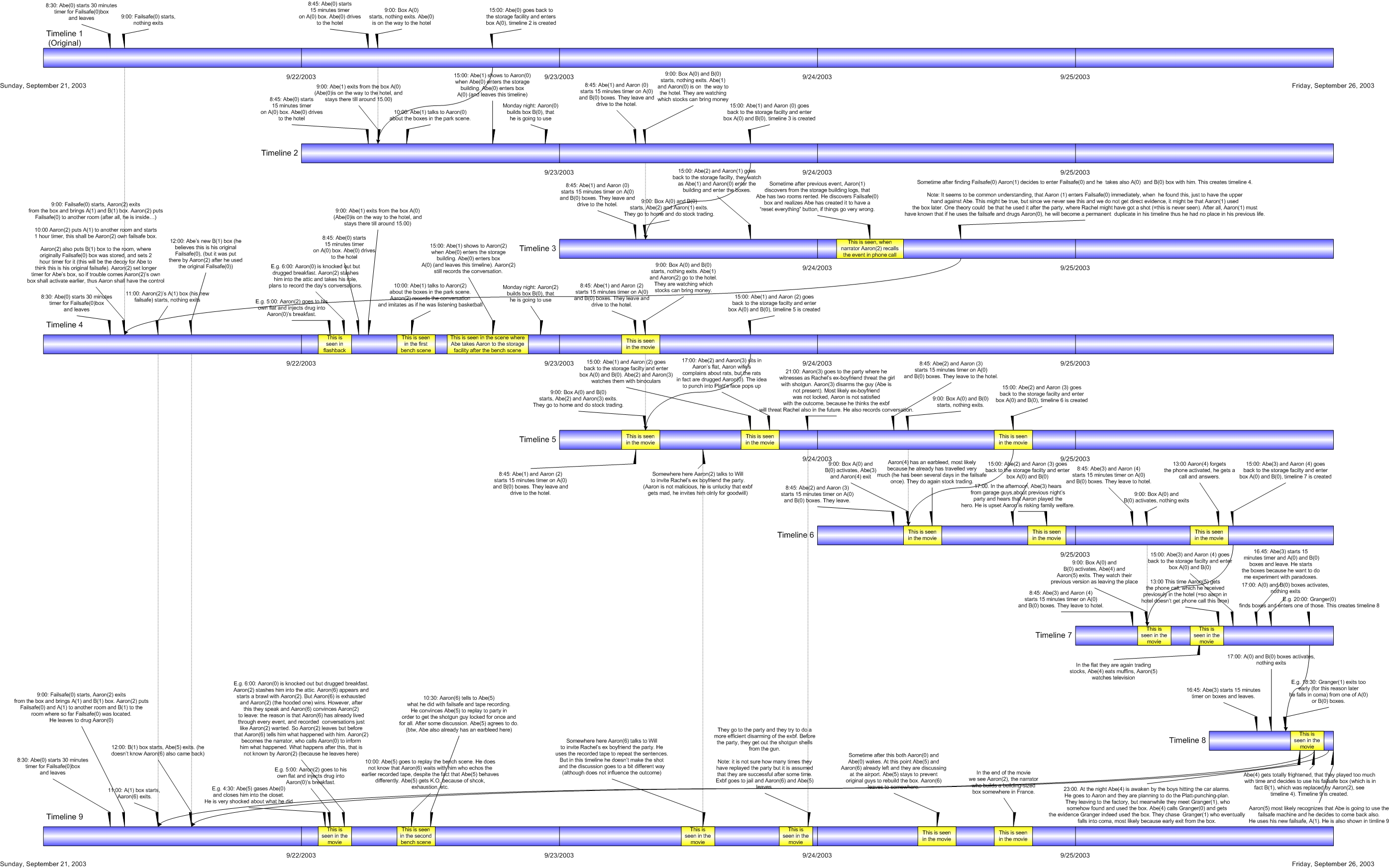
Wed Aug 26 Fri Aug 28 [lecture notes]

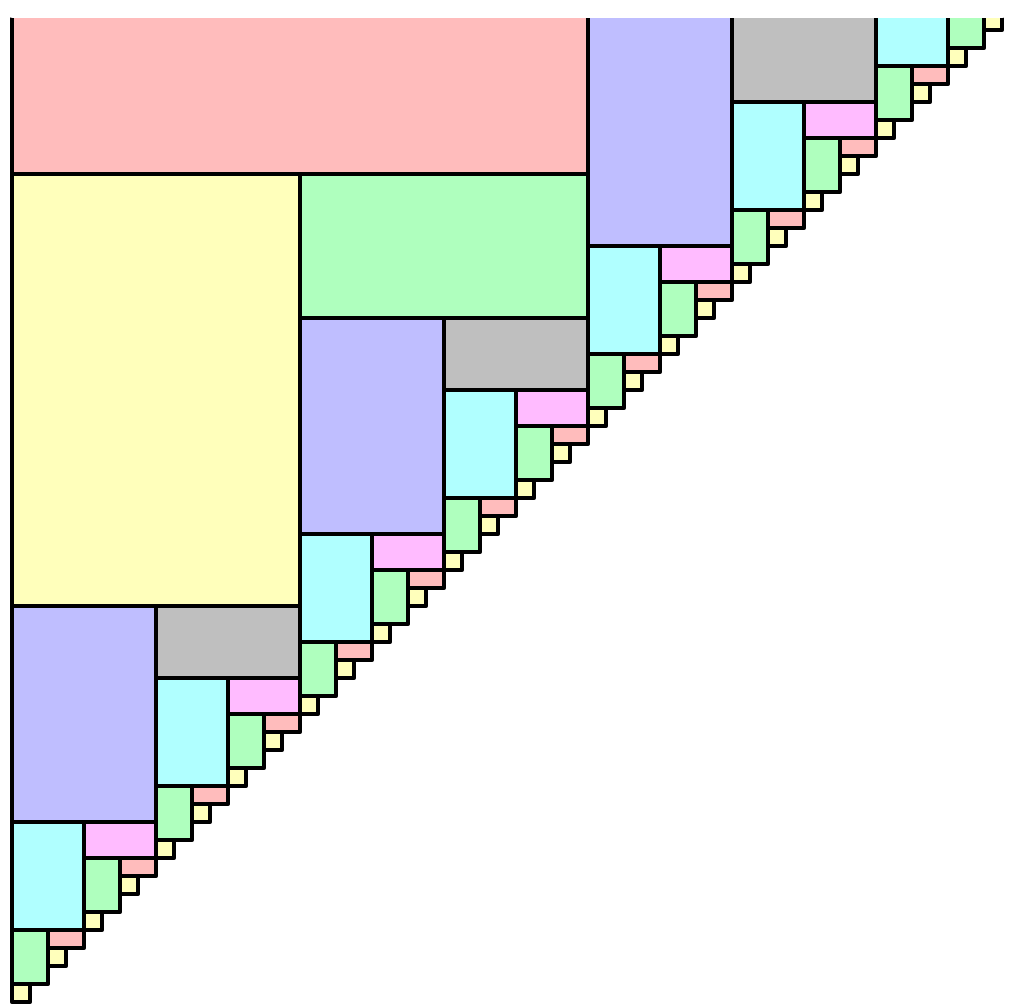
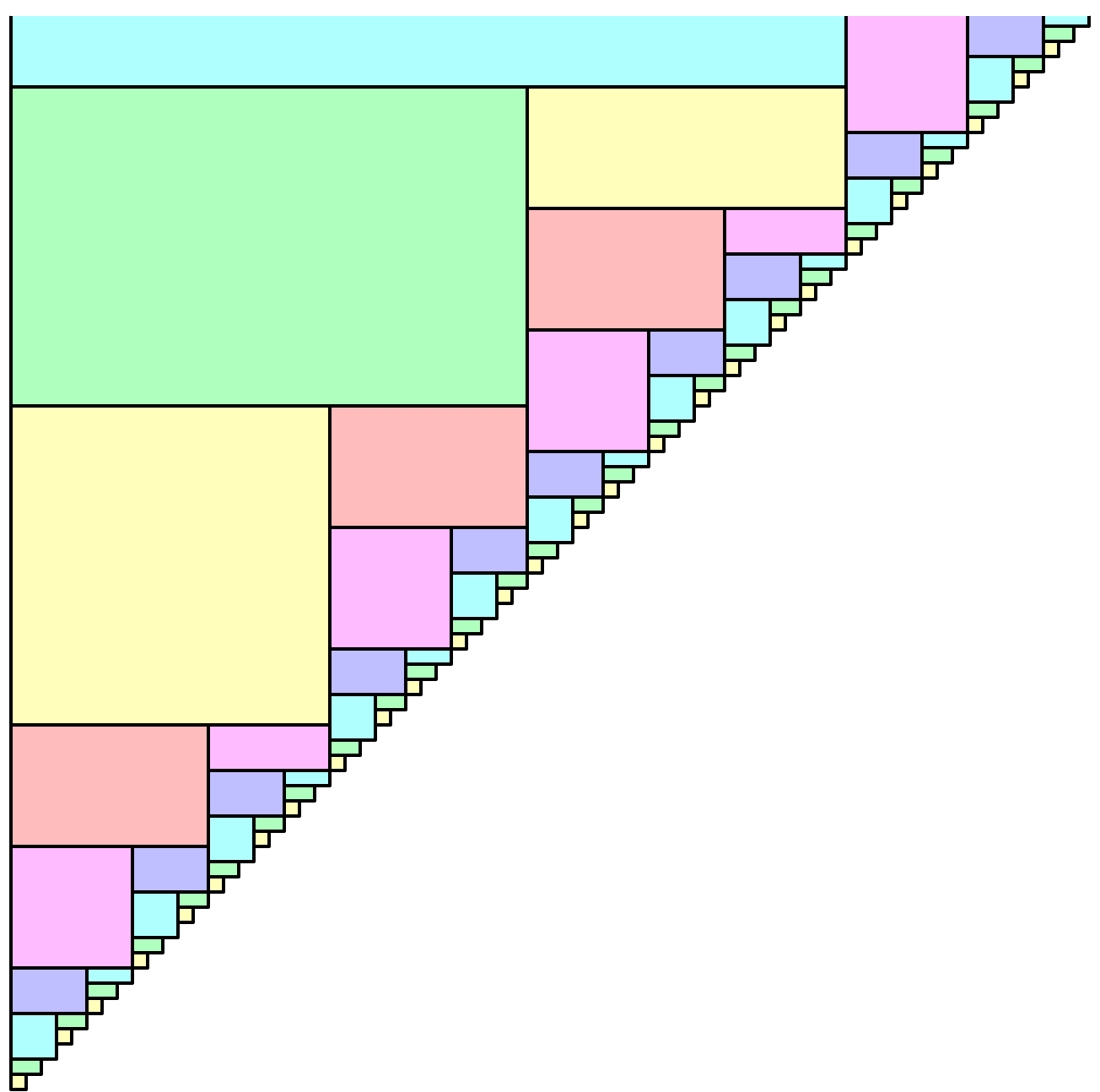
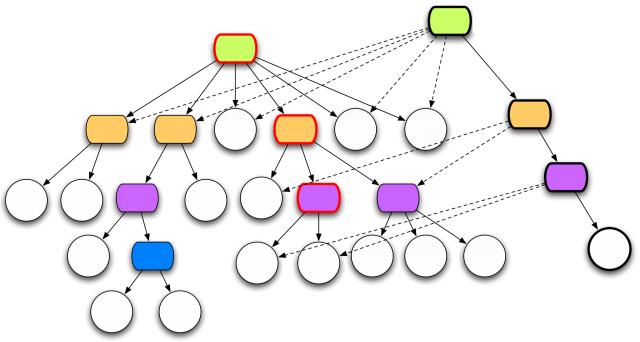
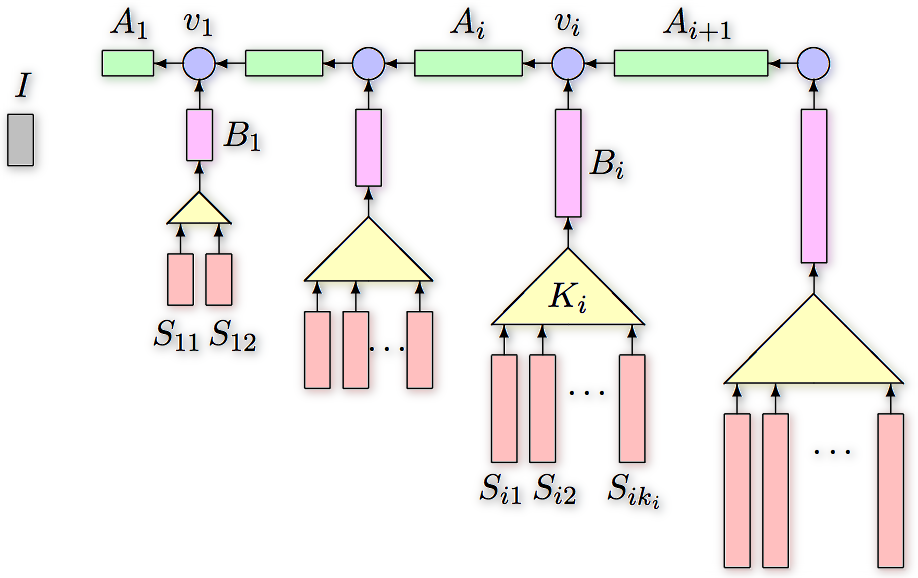
Decomposable searching problems: the Bentley-Saxe logarithmic method; local rebuilding; lazy deamortization; O(P(n)log n/n) worst-case insertion time; anti-data structures for invertible queries; weak deletions; (lazy) global rebuilding; O(P(n)log n/n) worst-case insertion time and O(P(n)/n + D(n)) worst-case deletion time.

References (click to show/hide)

Lazy binary and lazy Fibonacci counters
after [Bentley Saxe 1980]

Lars Arge and Jeffrey Scott Vitter. Optimal external memory interval management. SIAM J. Computing 32(6):1488–1508, 2003. [Among other results, describes weight-balanced B-trees, a prime example of a data structure that directly supports insertions and weak deletions.]
Jon L. Bentley. Decomposable searching problems. Information Processing Letters 8:244–251, 1979.
Jon L. Bentley. Multidimensional binary search trees used for associative searching. Communications of the ACM 18:509–517, 1975. [Introduces kd-trees, a prime example of a data structure that easily supports weak deletions, but not insertions or real deletions.]
Jon L. Bentley and James B. Saxe*. Decomposable searching problems: 1. Static-to-dynamic transformations. J. Algorithms 1(4):301–358, 1980. [Introduces the logarithmic method for adding insertion to any static data structure for a decomposable search problem.]
Michael J. Clancy* and Donald E. Knuth. A Programming and Problem-Solving Seminar. Stanford University Computer Science Department Report STAN-CS-77-606, April 1977. [One of the earliest examples of non-standard number systems being used to design efficient dynamic data structures—in this case, finger search trees.]
Kurt Mehlhorn. Lower bounds on the efficiency of transforming static data structures into dynamic data structures. Mathematical Systems Theory 15:1–16, 1981.
Kurt Mehlhorn. Data Structures and Algorithms III: Multi-dimensional Searching and Computational Geometry. EATCS Monographs, Springer, 1984. [Begins with a thorough overview of dynamization techniques for decomposable search problems. Still one of the best references for this material.]
Kurt Mehlhorn and Mark H. Overmars*. Optimal dynamization of decomposable search problems. Information Processing Letters 12:93–98, 1981.
Mark H. Overmars*. The Design of Dynamic Data Structures. Lecture Notes in Computer Science 156, Springer, 1983. [Mark's PhD thesis. Describes several families of methods for transforming static data structures into fully dynamic data structures, along with several geometric applications. Still one of the best references for this material.]
Mark H. Overmars* and Jan van Leeuwen. Two general methods for dynamizing decomposable searching problems. Computing 26:155–166, 1981. [Describes a lazy version of Bentley-Saxe to modify data structures that support weak deletions and insertions, so that they support real deletions.]
Mark H. Overmars* and Jan van Leeuwen. Worst-case optimal insertion and deletion methods for decomposable searching problems. Information Processing Letters 12(4):168–173, 1981. [Introduces the lazy local rebuilding technique for deamortizing Bentley-Saxe.]
Himanshu Suri and Victor Vazquez. Combination Pizza Hut and Taco Bell. Shut Up, Dude, 2010. [They're at the Pizza Hut. They're at the Taco Bell. They're at the combination Pizza Hut and Taco Bell. Nearest neighbor searching is a decomposable search problem over an idempotent but non-inversive semigroup.]

Wed Sep 2 Fri Sep 4 [lecture notes]

Scapegoat trees: O(log n) worst-case search and amortized update time using O(1) extra space

References (click to show/hide)

A well-balanced tree?
[Andersson, J. Alg. 1999]

Arne Andersson*. Improving partial rebuilding by using simple balance criteria. Proc. Workshop on Algorithms and Data Structures, 393–402. Lecture Notes in Computer Science 382, Springer, 1989. [The first discovery of scapegoat trees.]
Arne Andersson. General balanced trees. J. Algorithms 30:1–28, 1999. [The journal version of the previous paper.]
Arne Andersson and Tony W. Lai*. Fast updating of well-balanced trees. Proc. 2nd Scandinavian Workshop on Algorithm Theory 111–121. Lecture Notes in Computer Science 447, Springer, 1990. [Scapegoat trees with depth lg n+c require only O(log²n/c) amortized time per insertion or deletion, for any constant c. The amortized update time can be reduced to O(log n/c) using a standard indirection trick: replace the leaves of the scapegoat tree with perfectly balanced subtrees of size Θ(log n).]
Igal Galperin* and Ronald L. Rivest. Scapegoat trees. Proc. 4th th Annual ACM-SIAM Symposium on Discrete Algorithms, 165–174, 1993. [The second independent discovery of scapegoat trees and the origin of the name.]

Splay trees: rotations, roller-coasters and zig-zags, weighted amortized analysis, O(log n) amortized time, static optimality theorem, static and dynamic finger properties, working set property, dynamic optimality and other splay tree conjectures

References (click to show/hide)

A Self-Adjusting Search Tree
by Jorge Stolfi (1987)

Ranjan Chaudhuri and Hartmut Höft. Splaying a search tree in preorder takes linear time. International J. Mathematics and Mathematical Sciences 14(3):545–551, 1991. Also appeared in SIGACT News 24(2):88–93, 1993.
Richard Cole, Bud Mishra, Jeanette Schmidt, and Alan Siegel. On the dynamic finger conjecture for splay trees. Part I: Splay sorting log n-block sequences. SIAM J. Computing 30:1–43, 2000.
Richard Cole. On the dynamic finger conjecture for splay trees. Part II: The proof. SIAM J. Computing 30:44–85, 2000.
Amr Elmasry. On the sequential access theorem and deque conjecture for splay trees. Theoretical Computer Science 314(3):459–466, 2004. [Best upper bound known for the sequential access theorem: Accessing all n elements of a splay tree in increasing order requires at most 4.5n rotations.]
Seth Pettie. Splay trees, Davenport-Schinzel sequences, and the deque conjecture. Proc. 19th Annual ACM-SIAM Symposium on Discrete Algorithms 1115–1124, 2008. [Proves that n deque operations on an n-node splay tree require at most O(n α*(n)) time, where α*(n) is the iterated inverse Ackermann function. The paper includes a thorough survey of other splay tree results, up to 2008.]
Daniel D. Sleator and Robert E. Tarjan. Self-adjusting binary search trees. J. ACM 32:652-686, 1985. [HTML demo and C code] [The original splay tree paper.]
Rajamani Sundar*. On the deque conjecture for the splay algorithm. Combinatorica 12(1):95–124, 1992. [Proves that n deque operations on an n-node splay tree require at most O(n α(n)) time, where α(n) is the inverse Ackermann function.]
Robert E. Tarjan. Data Structures and Network Algorithms. CBMS-NSF Regional Conference Series in Applied Mathematics 44, SIAM, 1983. [Includes a chapter on splay trees. Yes, it took less time to publish an entire 130-page book than one 35-page journal paper.]
Robert E. Tarjan. Sequential access in splay trees takes linear time. Combinatorica 5:367–378, 1985. [Established the sequential access theorem: Accessing all n elements of a splay tree in increasing order requires O(n) time.]

Fri Sep 4 Wed Sep 9 [incomplete lecture notes]

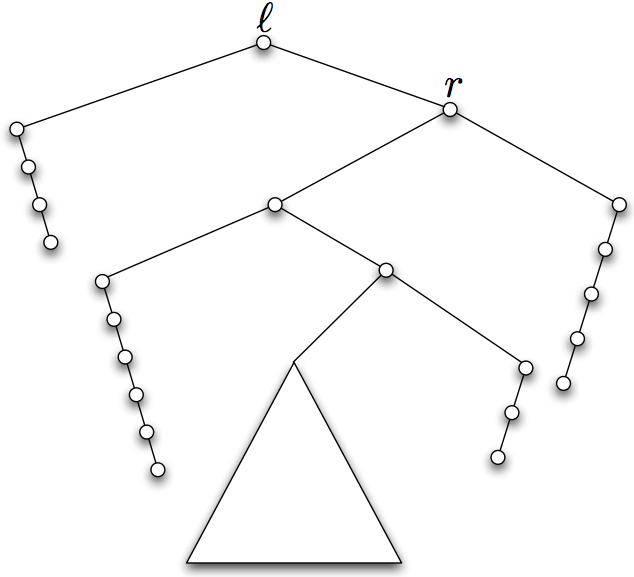
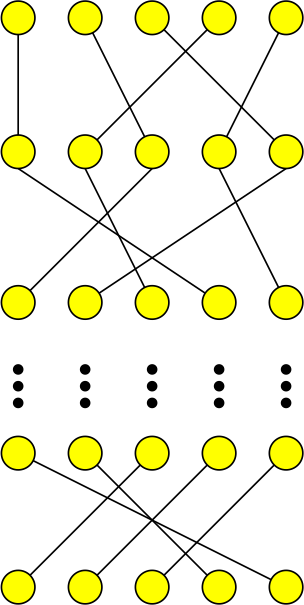
Lower bounds for dynamic binary search trees: arborally satisfied sets, independent rectangle lower bound, Wilber's interleave and alternation lower bounds, SIGNEDGREEDY lower bound, GREEDYFUTURE

References (click to show/hide)

GREEDYFUTURE in action
[Demaine et al., SODA 2009]

Parinya Chalermsook, Mayank Goswami, Laszlo Kozma, Kurt Mehlhorn, and Thatchaphol Saranurak. Self-Adjusting Binary Search Trees: What Makes Them Tick? Proc. 23rd European Symposium on Algorithms, 2015, to appear. arXiv:1503.03105.
Erik D. Demaine, Dion Harmon*, John Iacono, Daniel Kane*, and Mihai Pătraşcu. The geometry of binary search trees. Proc. 20th Annual ACM-SIAM Symposium on Discrete Algorithms 496–505, 2009. [Introduces arborally satisfied sets, and proves their equivalence to dynamic binary search trees. See also Derryberry et al. 2005.]
Jonathan Derryberry*, Daniel D. Sleator, and Chengwen Chris Wang*. A lower bound framework for binary search trees with rotations. Technical Report CMU-CS-05-187, Carnegie Mellon University, November 22, 2005. [A variant of the geometric view of dynamic binary search trees, developed independently from Demaine et al. 2009]
George F. Georgakopoulos. Splay trees: a reweighting lemma and a proof of competitiveness vs. dynamic balanced trees. J. Algorithms 51:64–76, 2004. [Defines a class of so-called parametrically balanced dynamic binary search tree and proves that splay trees are O(1)-competitive within this class.]
Dion Harmon*. New Bounds on Optimal Binary Search Trees. Ph.D. dissertation, Department of Mathematics, MIT, June 2006. [Describes the results in Demaine et al. 2009 in more detail, using slightly different terminology.]
John Iacono. Key independent optimality. Algorithmica, 42:3–10, 2005.
John Iacono. In pursuit of the dynamic optimality conjecture. Space-Efficient Data Structures, Streams, and Algorithms, 236–250, 2013. arXiv:1306.0207. [Surveys lower bound techniques and presents a dynamic BST that is optimal, assuming that an optimal dynamic BST exists at all.]
Joan M. Lucas. Canonical forms for competitive binary search tree algorithms. Tech. Rep. DCS-TR-250, Rutgers University, 1988. [Introduces an offline dynamic binary search tree algorithm, called GREEDYFUTURE by Demaine et al.; see also Munro 2000.]
J. Ian Munro. On the competitiveness of linear search. Proc. 8th Annual European Symposium on Algorithms 338–345. Lecture Notes in Computer Science 1879, Springer, 2000. [Independently describes the offline dynamic binary search tree algorithm called IAN (“Introduce As Necessary”) in Harmon's thesis and GREEDYFUTURE by Demaine et al.; see also Lucas 1988.]
Robert E. Wilber*. Lower bounds for accessing binary search trees with rotations. SIAM J. Computing 18(1):56-67, 1989. [Proves two important lower bounds on the total access cost of dynamic binary search trees.]

O(log log n)-competitive binary search trees: tango trees, multisplay trees, chain-splay trees, skip-splay trees, poketrees, zipper trees

References (click to show/hide)

Representation of a preferred path in a zipper tree
[Bose et al., SODA 2008]

Avrim Blum, Shuchi Chawla*, and Adam Kalai*. Static optimality and dynamic search-optimality in lists and trees. Algorithmica 36(3):249–260, 2003. [Describes a simple but computationally expensive dynamic binary search tree that is 14-competitive if the cost of rotations is ignored.]
Prosenjit Bose, Karim Douïeb*, and Stefan Langerman. Dynamic optimality for skip lists and B-trees. Proc. 19th Annual ACM-SIAM Symposium on Discrete Algorithms 1106–1114, 2008. [Proves that among “weakly bounded” skip lists, the working set bound is a lower bound on the access time, and describes a “weakly bounded” deterministic self-adjusting skip list whose access time is within a constant factor of the working set bound.]
Prosenjit Bose, Karim Douïeb, Vida Dujmović, and Rolf Fagerberg. An O(log log n)-competitive binary search tree with optimal worst-case access times. Proc. 12th Scandinavian Symposium and Workshops on Algorithm Theory, 38–49. Lecture Notes in Computer Science 6139, Springer, 2010. [Zipper trees, a O(log log n)-competitive dynamic binary search tree.]
Parinya Chalermsook, Mayank Goswami, Laszlo Kozma, Kurt Mehlhorn, and Thatchaphol Saranurak. Self-Adjusting Binary Search Trees: What Makes Them Tick? Proc. 23rd European Symposium on Algorithms, 2015, to appear. arXiv:1503.03105.
Erik D. Demaine, Dion Harmon*, John Iacono, and Mihai Pătraşcu. Dynamic optimality—almost. SIAM J. Computing 37(1):240–251, 2007. [Tango trees, the first O(log log n)-competitive dynamic binary search tree. Only competitive for searches, not for insertions or deletions.]
Jonathan Derryberry* and Daniel D. Sleator. Skip-splay: Toward achieving the unified bound in the BST model. Proc. Workshop on Algorithms and Data Structures, 194–205. Lecture Notes in Computer Science 5664, Springer, 2009. [Another O(log log n)-competitive dynamic binary search tree.]
George F. Georgakopoulos. Chain-splay trees, or, how to achieve and prove log log n-competitiveness by splaying. Information Processing Letters 106(1):37–43, 2008. [Another O(log log n)-competitive dynamic binary search tree, based on splaying.]
John Iacono. Alternatives to splay trees with O(log n) worst-case access times. Proc. 12th Annual ACM-SIAM Symposium on Discrete Algorithms, 516–522. [Defines the unified bound, and describes a dynamic dictionary (but not a binary search tree) that satisfies it.]
Jussi Kujala* and Tapio Elomaa. Poketree: A dynamically competitive data structure with good worst-case performance. Proc. 17th International Symposium on Algorithms and Computation, 277–288. Lecture Notes in Computer Science 4288, Springer, 2006. [A O(log log n)-competitive dynamic data structure with O(log n) worst-case access time, but strictly speaking not a dynamic binary search tree.]
Chengwen Chris Wang*. Jonathan Derryberry*, and Daniel D. Sleator. O(log log n)-competitive binary search trees. Proc. 17th Annual ACM-SIAM Symposium on Discrete Algorithms, 374-383, 2006. [Multisplay trees, the first O(log log n)-competitive dynamic binary search tree that competitively supports insertions and deletions.]
Chengwen Chris Wang*. Multi-Splay Trees. Ph.D. dissertation, Department of Computer Science, Carnegie Mellon University, July 2006.

Fri Sep 11 Wed Sep 16

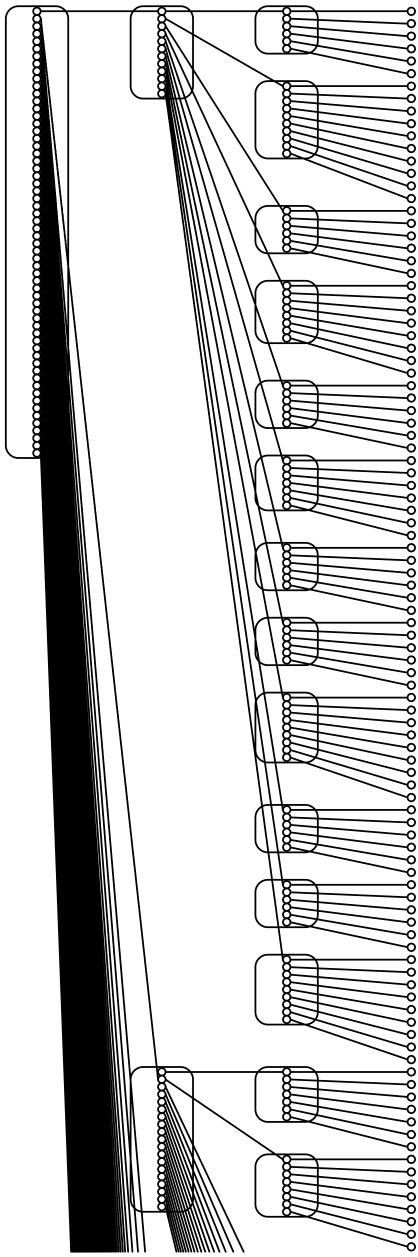
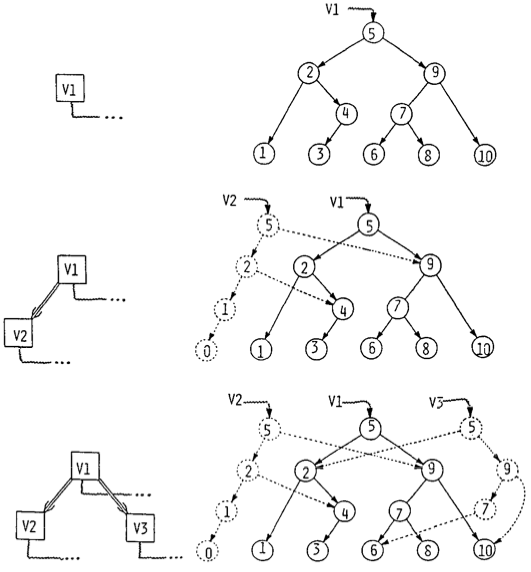
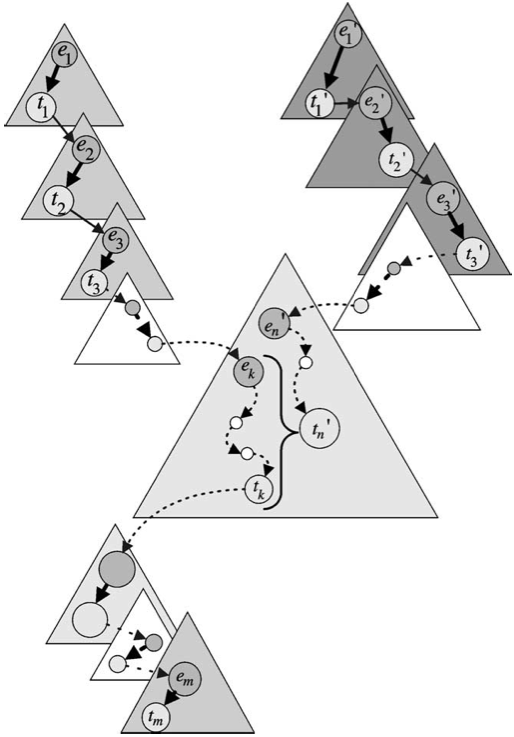
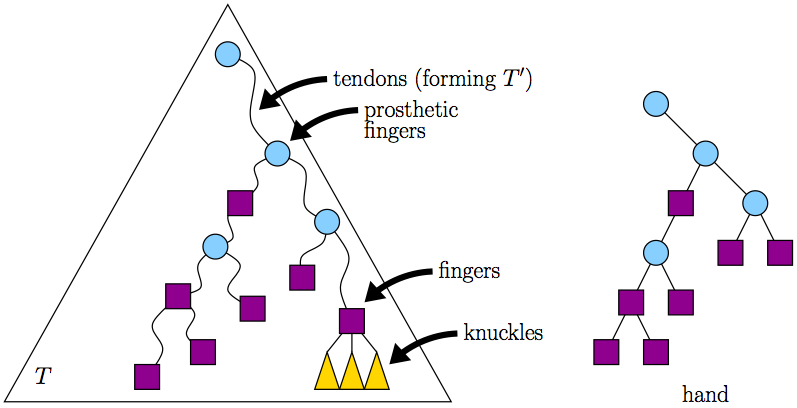
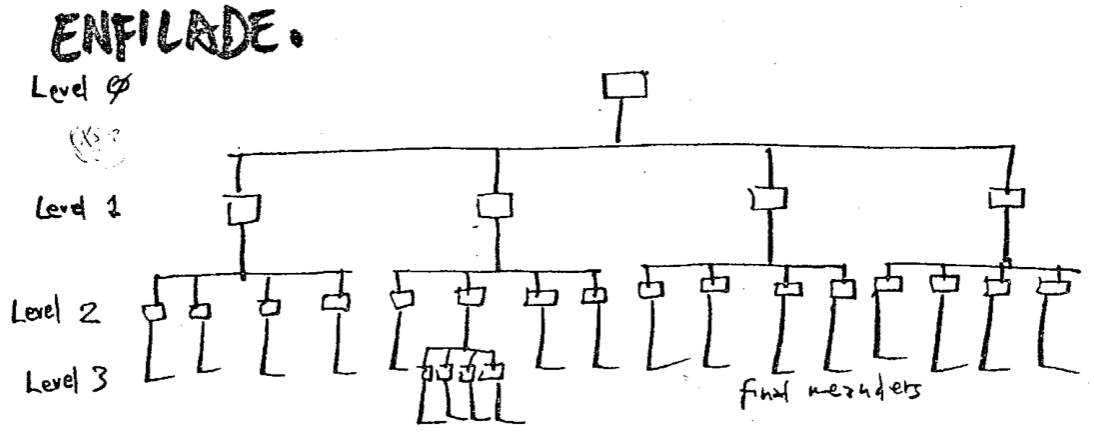
Dynamic forest maintenance: Link-cut trees; CUT, JOIN, and FINDROOT in O(log n) amortized time; path queries and updates in O(log n) amortized time via lazy propagation; Euler-tour trees; subtree queries and updates in O(log n) amortized time; sketches of topology trees, top trees, rake-compress trees, and self-adjusting top trees.

References (click to show/hide)

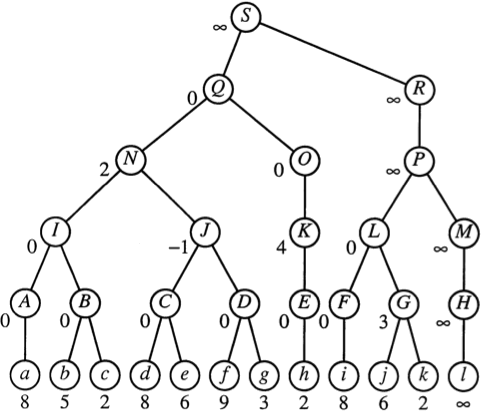
A multilevel partition of an edge-weighted binary tree, and the resulting topology tree.
[Frederickson 1997]

Umut A. Acar*, Guy E. Blelloch, Robert Harper, Jorge L. Vittes*, and Shan Leung Maverick Woo*. Dynamizing static algorithms, with applications to dynamic trees and history independence. Proc. 15th Annual ACM-SIAM Symposium on Discrete Algorithms, 531–540, 2004. [Rake-compress trees.]
Stephen Alstrup, Jacob Holm*, Kristian de Lichtenberg*, and Mikkel Thorup. Maintaining information in fully dynamic trees with top trees. ACM Transactions on Algorithms 1(2):243–264, 2005.
David Eisenstadt. dtree: Dynamic trees à la carte. Last revised May 2014. Last accessed September 2015. [A C++ implementation of Sleator-Tarjan link-cut trees with (optional) support for subtree operations.]
David Eisenstadt. mississippi: Multiple-source shortest paths and betweenness centrality in planar graphs. Last revised April 2014. Last accessed September 2015. [Includes a lightweight 80-line C implementation of Sleator-Tarjan link-cut trees.]
Greg Frederickson. Data structures for on-line updating of minimum spanning trees, with applications. SIAM J. Computing 14:781–798, 1985. [Topology trees.]
Greg Frederickson. A data structure for dynamically maintaining rooted trees. J. Algorithms 24:37–65, 1997. [Directed topology trees.]
Andrew V. Goldberg, Michael D. Grigoriadis, and Robert E. Tarjan. Use of dynamic trees in a network simplex algorithm for the maximum flow problem. Mathematical Programming 50(1–3):277–290, 1991. [Added subtree operations to link-cut trees.]
Monika Rauch Henzinger and Valerie King. Randomized fully dynamic graph algorithms with polylogarithmic time per operation. J. ACM 46:502–516, 1999. [Euler-tour trees; see also Tarjan 1997.]
Gary L. Miller and John H. Reif. Parallel tree contraction and its application. Proc. 26th Annual IEEE Symposium on Foundations of Computer Science, 478–489, 1985. [Introduces the rake and compress operations in the context of parallel algorithms.]
Gary L. Miller and John H. Reif. Parallel tree contraction part 1: Fundamentals. Randomness and Computation, 47–72. Silvio Micali, editor. Advances in Computing Research 5, JAI Press, 1989. [Full version of the previous paper.]
Daniel D. Sleator* and Robert E. Tarjan. A data structure for dynamic trees. J. Computer and System Sciences 26:362–391, 1983. [The original formulation of link-cut trees via biased trees, with O(log n) worst-case operation time. Uses dynamic trees to obtain the first maximum-flow algorithm that runs in O(mn log n) time, based on blocking flows.]
Robert E. Tarjan. Data Structures and Network Algorithms. CBMS-NSF Regional Conference Series in Applied Mathematics 44, SIAM, 1983. [Includes a chapter on link-cut trees, reformulated to use splay trees.]
Robert E. Tarjan. Efficiency of the primal network simplex algorithm for the minimum-cost circulation problem. Mathematics of Operations Research 16(2):272–291, 1991. [Added directed-path operations to link-cut trees.]
Robert E. Tarjan. Dynamic trees as search trees via euler tours, applied to the network simplex algorithm. Mathematical Programming 78(2):169–177, 1997. [Euler-tour trees; see also Henzinger and King 1999.]
Robert E. Tarjan and Uzi Vishkin. An efficient parallel biconnectivity algorithm. SIAM J. Computing 14(4):862—874, 1985. [Introduces the Euler tour technique in the context of parallel algorithms.]
Robert E. Tarjan and Renato Werneck*. Self-adjusting top trees. Proc. 16th Annual ACM-SIAM Symposium on Discrete Algorithms, 813–822, 2005.
Robert E. Tarjan and Renato Werneck*. Dynamic trees in practice. J. Experimental Algorithmics 14, article 4.5, 2009. [Compares several dynamic forest structures, including Euler-tour trees, rake-compress trees, splay-based link-cut trees, top trees, self-adjusting top trees, and a brute-force link-cut tree with only parent pointers. For small graphs (up to a few thousand vertices), brute force wins. For larger graphs, link-cut trees win in applications with more links and cuts, there is no clear winner in applications with more queries. Really, ACM, what is this "Article 4.5" nonsense?]

Fri Sep 18 Wed Sep 23

Applications of dynamic trees: Maximum flows via network simplex; parametric and multiple-source shortest paths; dynamic graph connectivity

References (click to show/hide)

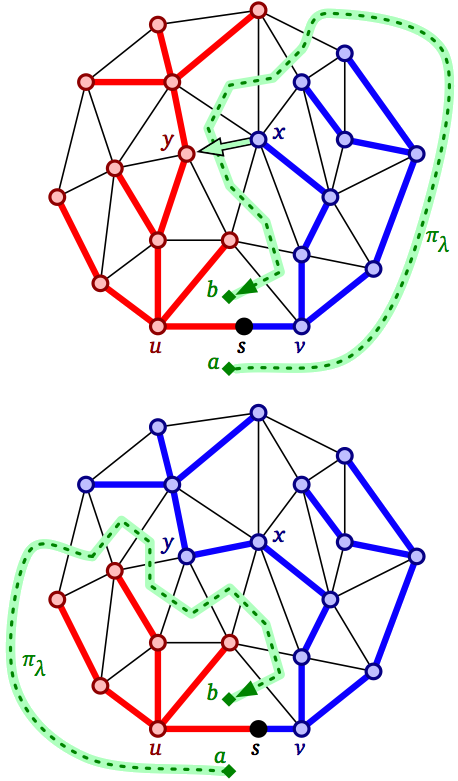
An edge pivots into a planar shortest-path tree as the source node moves along an edge.
[Chambers Cabello Erickson 2007]

Glencora Borradaile* and Philip Klein. An O(n log n) algorithm for maximum st-flow in a directed planar graph. J. ACM 56(2), article 9, 2009. [Does what it says on the tin.]
Sergio Cabello, Erin W. Chambers*, and Jeff Erickson. Multiple source shortest paths in embedded graphs. SIAM Journal on Computing 42(4):1542–1571, 2013. [Generalizes Klein's planar multiple-source shortest path algorithm for planar graphs to graphs embedded on more general surfaces.]
David Eppstein. Dynamic generators of topologically embedded graphs. Proc. 14th Annual ACM-SIAM Symposium on Discrete Algorithms 599–608, 2003. [Uses Thorup's dynamic connectivity data structure to dynamically maintain the generators of a fundamental group of a surface represented by a rotation system of a graph. Introduces tree-cotree decompositions for surface graphs. Those two sentences should make sense if you took my computational topology class last year.]
Jeff Erickson. Maximum flows and parametric shortest paths in planar graphs. Proc. 21st Annual ACM-SIAM Symposium on Discrete Algorithms 794–804, 2010. [Expresses and reanalyzes Borradaile and Klein's planar maximum-flow algorithm in terms of parametric shortest paths.]
Andrew V. Goldberg, Michael D. Grigoriadis, and Robert E. Tarjan. Use of dynamic trees in a network simplex algorithm for the maximum flow problem. Mathematical Programming 50(1–3):277–290, 1991. [Used dynamic trees to obtain another maximum-flow algorithm that runs in O(mn log n) time, based on network simplex, using a pivot rule of Goldfarb and Hao.]
Monika Rauch Henzinger and Valerie King. Randomized fully dynamic graph algorithms with polylogarithmic time per operation. J. ACM 46:502–516, 1999. [Edge insertions and edge deletions in O(log³ n) amortized expected time, and connectivity queries in O(log n/log log n) time.]
Jacob Holm*, Kristian de Lichtenberg*, Mikkel Thorup. Poly-logarithmic deterministic fully-dynamic algorithms for connectivity, minimum spanning tree, 2-edge, and biconnectivity. J. ACM 48(4):723-760, 2001. [Edge insertions and edge deletions in O(log² n) time and connectivity queries in O(log n/log log n) time.]
Raj D. Iyer, Jr.*, David Karger, Hariharan S. Rahul*, and Mikkel Thorup. An experimental study of polylogarithmic, fully dynamic, connectivity algorithms. J. Experimental Algorithmics 6, article 4, 2001.
Philip Klein. Multiple-source shortest paths in planar graphs. Proc. 16th Annual ACM-SIAM Symposium on Discrete Algorithms 146–155, 2005. [Implicitly computes all shortest-path trees rooted on a single face of a planar graph in O(n log n) time. Stores both the shortest path tree and the dual cotree in dynamic tree data structures.]
Robert E. Tarjan. Dynamic trees as search trees via euler tours, applied to the network simplex algorithm. Mathematical Programming 78(2):169–177, 1997. [Simplifies the O(mn log n)-time network-simplex maximum-flow algorithm of Goldberg, Grigoriadis, and Tarjan using Euler-tour trees.]
Mikkel Thorup. Near-optimal fully-dynamic graph connectivity. Proc. 32nd Annual Acm Symposium on Theory of Computing, 343–350, 2000. [Edge insertions and edge deletions in O(log n (log log n)³) time and connectivity queries in O(log n/log log log n) time, almost matching the Ω(log n) lower bound.]

Fri Sep 25

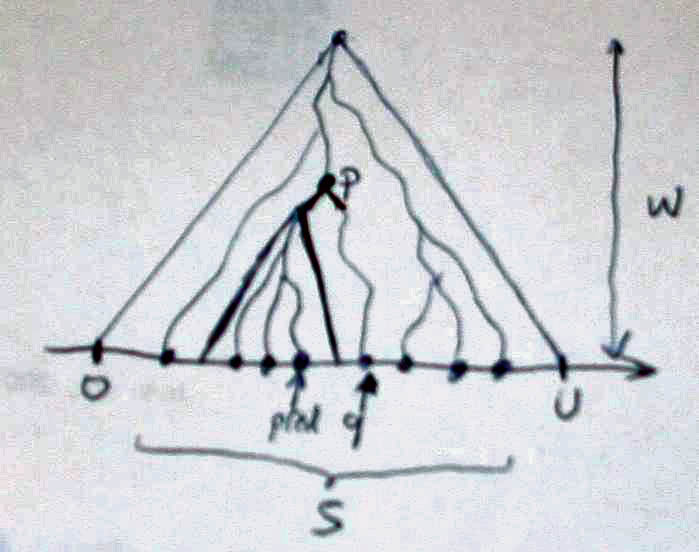
Lower bounds for dynamic connectivity: Cell probe model, prefix sums, reductions, time trees, non-deterministic encoding

References (click to show/hide)

Reducing dynamic prefix-sum to dynamic connectivity
[Demaine Pǎtraşcu 2006]

Michael L. Fredman and Monika Rauch Henzinger. Lower bounds for fully dynamic connectivity problems in graphs. Algorithmica 22(3):351–362, 1998. [Among other results, observes an easy reduction from parity prefix sums to dynamic reachability. See also Miltersen et al. 1994.]
Michael L. Fredman and Michael E. Saks. The cell probe complexity of dynamic data structures. Proc. 21st ACM Symposium on Theory of Computing, 345–354, 1989. [Introduces the chronogram technique for proving cell=probe lower bounds. Proves an Ω(log n/log log n) lower bound for dynamic parity prefix sum.]
Peter Bro Miltersen. Cell probe complexity: A survey. Manuscript, 2000. Invited talk/paper at Advances in Data Structures, a pre-conference workshop of FSTTCS'99. [Powerpoint slides]
Peter Bro Miltersen, Sairam Subramanian*, Jeffrey Scott Vitter, and Roberto Tamassia, Complexity models for incremental computation. Theoretical Computer Science 130(1):203–236, 1994. [Among other results, observes an easy reduction from parity prefix sums to dynamic reachability. See also Fredman and Henzinger 1998.]
Mihai Pătraşcu. Lower bounds for dynamic connectivity. Encyclopedia of Algorithms, 463–477. Springer, 2008. [Overview of the author's two Ω(log n) cell-probe lower bound proofs.]
Mihai Pătraşcu. Unifying the landscape of cell-probe lowerbounds. SIAM J. Computing 40(3): 827–847, 2011. [Proves several cell-prove lower bounds, including an Ω(log n/log log n) lower bound for dynamic connectivity, via reductions from lopsided set disjointness.]
Mihai Pătraşcu* and Erik D. Demaine. Logarithmic lower bounds in the cell-probe model. SIAM J. Computing 35(4):932–963, 2006. [Proves Ω(log n) cell-probe lower bound for dynamic connectivity (by reduction from partial sums) using the “time tree” technique.]
Mihai Pătraşcu* and Corina E. Tarniţă*. On dynamic bit-probe complexity. Theoretical Computer Science 380, 2007. [Reproves Ω(log n) cell-probe lower bound for dynamic connectivity (by reduction from partial sums) using a modification of Fredman and Saks' chronogram technique.]
Andrew Chi-Chih Yao. Should tables be sorted? J. ACM 28(3):615–628, 1981. [Formally introduces the cell-probe model of computation. The answer is “Not if you can hash.”]

Wed Sep 30 Fri Oct 1

Efficient priroty queues: Implicit d-ary heaps, Fibonacci heaps, pairing heaps, rank-pairing heaps

Historical references (click to show/hide)

An implicit binary tree [Eytzinger 1590]

Clark A. Crane*. Linear lists and priority queues as balanced binary trees. Ph.D. thesis, Computer Science Department, Stanford University, 1972. Technical Report STAN-CS-72-259, [Leftist heaps, the first priority queue to support Meld in O(log n) time.]
Michaël Eytzinger. Thesavrvs principvm hac ætate in Evropa viventium. Kempensem, Köln, 1590. [The first use of implicit binary trees.]
Robert W. Floyd. Algorithm 113: Treesort. Communications of the ACM 5(8):434, 1962. [An early version of heapsort, which used an array as an implicit tournament tree.]
Robert W. Floyd. Algorithm 245: Treesort 3. Communications of the ACM 7(12):701, 1964. [The algorithm now universally known as heapsort, including a linear-time in-place algorithm for building an implicit binary heap from an unsorted array.]
David B. Johnson. Priority queues with update and finding minimum spanning trees. Information Processing Letters 4(3):53–57, 1975. [Implicit d-ary heaps.]
John W. J. Williams. Algorithm 232: Heapsort. Communications of the ACM 7(6):347–348, 1964. [Array-based implicit heaps, and possibly the first use of the word “heap” to mean a data structure implementing a priority queue.]

Fibonacci heap references (click to show/hide)

Boarding Group 1

Gerth Stølting Brodal*. Worst-case efficient priority queues. Proc. 7th ACM-SIAM Symposium on Discrete Algorithms, 52–58, 1996. [The first priority queue whose worst-case time bounds match the amortized time bounds of Fibonacci heaps.]
Gerth Stølting Brodal, George Lagogiannis, and Robert E. Tarjan. Strict Fibonacci heaps. Proc. 44th ACM Symposium on Theory of Computing 1177--1184, 2012. [The first pointer-based priority queue whose worst-case time bounds match the amortized time bounds of Fibonacci heaps.]
Timothy Chan. Quake heaps: A simple alternative to Fibonacci heaps. Space-Efficient Data Structures, Streams, and Algorithms: 27-32. Lecture Notes in Computer Science 8066, Springer, 2013.
James R. Driscoll, Harold N. Gabow, Ruth Shrairman, and Robert E. Tarjan. Relaxed heaps: An alternative to Fibonacci heaps with applications to parallel computation. Commununications of the ACM 31(11):1343–1354, 1988. [Frankie say the heap property doesn't always have to be satisfied everywhere.]
Stefan Edelkamp. Rank-relaxed weak queues: Faster than pairing and Fibonacci heaps? Technical report 54, TZI, Universität Bremen, 2009. [Answer: Only if you don't need DecreaseKey.]
Stefan Edelkamp, Amr Elmasry, Jyrki Katajainen, and Armin Weiß. Weak heaps and friends: Recent developments. Proc. 24th International Workshop on Combinatorial Algorithms 1–6. Lecture Notes in Computer Science 8288, Springer, 2013. [A brief survey of descendants of Dutton's weak heaps.]
Stefan Edelkamp, Amr Elmasry, and Jyrki Katajainen. The weak-heap family of priority queues in theory and praxis. Proc. 18th Computing: The Australasian Theory Symposium, 103–112, 2012.
Amr Elmasry. The violation heap: A relaxed Fibonacci-like heap. Proc. 16th Annual International Conference on Computing and Combinatorics 479–488, 2010.
Michael L. Fredman and Robert E. Tarjan. Fibonacci heaps and their uses in improved network optimization algorithms. J. Association for Computing Machinery 34(3):596–615, 1987. [The original Fibonacci heap paper.]
Bernard Haeupler*, Siddhartha Sen*, and Robert E. Tarjan. Rank-pairing heaps. SIAM J. Computing 40(6):1463–1485, 2011. [Lazy binomial queues with pairing by rank and rank-adjustment. Following the Red Herring Principle, rank-pairing heaps are not actually a variant of pairing heaps; by analogy, Fibonacci heaps should be called “degree-pairing heaps”.]
Peter Høyer. A general technique for implementation of efficient priority queues. Proc. 3rd Israel Symposium on Theory of Computer Systems, 57–66, 1995. [Just what it says on the tin. Red-black heaps and mergeable double-ended priority queues.]
Haim Kaplan and Robert E. Tarjan. Thin heaps, thick heaps. ACM Transactions on Algorithms 4(1), Article 3, 2008.
Daniel H. Larkin*, Siddhartha Sen*, Robert E. Tarjan. A back-to-basics empirical study of priority queues. Proc. 16th Workshop on Algorithm Engineering and Experiments, 61–72, 2014. arXiv:1403.0252. Code available at https://code.google.com/p/priority-queue-testing/. [Implicit d-ary heaps and pairing heaps are the best choices in practice. Binomial and Fibonacci heaps are next best. Everything else sucks.]
Daniel D. Sleator* and Robert E. Tarjan. Self-adjusting heaps. SIAM J. Computing 15(1):52–69, 1986. [Skew heaps, otherwise known as self-adjusting leftist heaps.]
Tadao Takaoka. Theory of 2-3 heaps. Discrete Applied Mathematics 126(1):115–128, 2003.
Tadao Takaoka. Theory of trinomial heaps. Proc. 6th Annual Int. Conf. Computing and Combinatorics, 362-372. Lecture Notes in Computer Science 1858, 2000.
Jean Vuillemin. A data structure for manipulating priority queues. Communications of the ACM 21, 309–314, 1978. [Binomial “queues”.]

Pairing heap references (click to show/hide)

Beer and cheese pairing

Ronald D. Dutton. Weak-heap sort. BIT 33(3):372–381, 1993. [Weak heaps, a clever implicit variant of binomial queues. Roughly a factor of 2 faster than standard binary heaps, at the cost of one extra bit per item.]
Amr Elmasry. Pairing heaps with O(log log n) decrease cost. Proc. 20th Annual ACM-SIAM Symposium on Discrete Algorithms, 471–476, 2000. [A variant of pairing heaps that is not covered by Fredman's lower bound.]
Amr Elmasry. Pairing heaps, scrambled pairing and square-root trees. International J. Computer Mathematics 87(14):3096–3110, 2010. [A pairing heap with a bad pairing strategy can require Ω(√n) amortized time per operation.]
Michael L. Fredman. On the efficiency of pairing heaps and related data structures. J. ACM 46(4):473–501, 1999. [Pairing heaps require Ω(log log n) amortized time for DecreaseKey.]
Michael L. Fredman, Robert Sedgewick, Daniel D. Sleator*, and Robert E. Tarjan. The pairing heap: A new form of self-adjusting heap. Algorithmica 1(1):111–129, 1986.
John Iacono. Improved upper bounds for pairing heaps. Proc. 7th Scandinavian Workshop on Algorithm Theory, 63--77. Lecture Notes in Computer Science 1851, Springer, 2000. arXiv:1110.4428.
Daniel H. Larkin*, Siddhartha Sen*, Robert E. Tarjan. A back-to-basics empirical study of priority queues. Proc. 16th Workshop on Algorithm Engineering and Experiments, 61–72, 2014. arXiv:1403.0252. Code available at https://code.google.com/p/priority-queue-testing/. [Implicit d-ary heaps and pairing heaps are the best choices in practice. Binomial and Fibonacci heaps are next best. Everything else sucks.]
Seth Pettie. Towards a final analysis of pairing heaps. Proc. 46th Annual IEEE Symposium on Foundations of Computer Science, 174–183, 2005. [O(2^{2 sqrt{log log n}}) amortized time for Insert, Meld, and DecreaseKey. Not universally believed.]

Fun with Tables

Wed Oct 6 Fri Oct 8 [lecture notes]

Basic hash tables: moments and tail inequalities, chaining, “perfect” hashing, linear probing; ran out of time for cuckoo hashing

Basic hashing references (click to show/hide)

Perfect hash browns.
The secret is to get all the moisture out of the potatoes.

Yossi Azar, Andrei Z. Broder, Anna R. Karlin, and Eli Upfal. Balanced allocations. SIAM J. Computing 29(1):180–200, 1999. [The power of two choices. In a chained hash table with two hash functions, where new items are always inserted into the smaller of the two chains, the expected length of the longest chain is only O(log log n).]
Andrei Z. Broder and Anna R. Karlin. Multilevel adaptive hashing. Proc. 1st Annual ACM-SIAM Symposium on Discrete Algorithms 43-53, 1990. [Maintain O(log log n) hash tables, where the ith table has size O(n/2ⁱ), and insert each new item into the minimum-index table where the item's slot is empty.]
Martin Dietzfelbinger, Anna Karlin*, Kurt Mehlhorn, Friedhelm Meyer auf der Heide, Hans Rohnert*, and Robert E. Tarjan. Dynamic perfect hashing: Upper and lower bounds. SIAM J. Computing 23(4):738–761, 1994. [Proves that the Fredman-Komlós-Szemerédi “perfect” hashing scheme can be made dynamic with O(1) expected amortized update time. Also proves under reasonable assumptions that any deterministic update algorithm requires Ω(log n) amortized time.]
Arnold I. Dumey. Indexing for rapid random-access memory. Computers and Automation 5(12):6–9, 1956. [The first published paper on hashing, although he didn't call it that. According to Knuth, hashing was described in several earlier internal IBM technical reports, but those reports were never published, so I can't cite them.]
Michael L. Fredman, János Komlós, and Endre Szemerédi. Storing a sparse table with O(1) worst-case access time. J. ACM 31(3):538–544, 1984. [Introduced static “perfect” hashing.]
Gaston H. Gonnet. Expected length of the longest probe sequence in hash code searching. J. ACM 28:289–304, 1981. [“Balls and bins” analysis of chaining, via approximation by a Poisson distribution.]
Donald E. Knuth*. Notes on ”open” addressing. Unpublished memorandum. July 22, 1963. [pdf version] [The first theoretical analysis of linear probing, and Knuth's first analysis of an algorithm. Yes, he was a student, but just barely.]
Anna Pagh, Rasmus Pagh, and Milan Ružić*. Linear probing with constant independence. SIAM J. Computing 39(3):1107–1120, 2009. [Easier analysis of linear probing.]
W. W. Peterson. Addressing for random-access storage. IBM J. Research and Development 1:130–146, 1957. [First published analysis of linear probing.]

Cuckoo hashing references (click to show/hide)

Coo Coo Comics #36 (1942)

A cuckoo clock

Luc Devroye and Pat Morin. Cuckoo hashing: Further analysis. Information Processing Letters 86(4):215–219, 2003.
Martin Dietzfelbinger and Christoph Weidling. Balanced allocation and dictionaries with tightly packed constant size bins. Theoretical Computer Science 380:47–68, 2007. [Extends cuckoo hashing to store n keys in (1+ε)n memory cells, using only two hash functions, by storing O(log(1/ε)) items in each bin instead of just one. Compare Fotakis et al. 2005.]
Dimitris Fotakis, Rasmus Pagh, Peter Sanders, and Paul Spirakis. Space efficient hash tables with worst-case constant access time. Theory of Computing Systems 38:229–248, 2005. [Extends cuckoo hashing to store n keys in (1+ε)n memory cells, using O(log(1/ε)) hash functions instead of just two. Compare Dietzfelbinger and Weidling 2007.]
Alan Frieze, Páll Melsted*, and Michael Mitzenmacher. An analysis of random-walk cuckoo hashing. Proc. 12th International Workshop on Approximation Algorithms in Combinatorial Optimization (APPROX), 350–364. Lecture Notes in Computer Science 5687, 2009. [Proves that the insertion time for cuckoo hashing with d>2 hash functions is polylogarithmic with high probability (unless the table load is very close to 1), if insertions are performed by a random walk in the cuckoo graph.]
Adam Kirsch* and Michael Mitzenmacher. The power of one move: Hashing schemes for hardware. IEEE/ACM Transactions on Networking 18(6):1752–1765, 2010.
Adam Kirsch*, Michael Mitzenmacher, and Udi Wieder. More robust hashing: Cuckoo hashing with a stash. SIAM J. Computing 39(4):1543–1561, 2009. Reinhard Kutzelnigg. Bipartite random graphs and cuckoo hashing. Proc. 4th Colloquium on Mathematics and Computer Science 403–406, 2006. –>
Michael Mitzenmacher. Some open questions related to cuckoo hashing. Proc. 17th Annual European Symposium on Algorithms 1–10. Lecture Notes in Computer Science 5757, Springer, 2009.
Rasmus Pagh* and Flemming Friche Rodler. Cuckoo hashing. J. Algorithms 51(2):122-144, 2004. [There's a sad sort of clanging from the clock in the hall / And the bells in the steeple too / And up in the nursery an absurd little bird / Is popping out to say cuckoo]

Good hash functions: Uniform versus k-universality vs k-independent vs ideal, polynomial hashing, tabulation hashing, tabulation with guaranteed independence, tail bounds without independence

References (click to show/hide)

J. Lawrence Carter and Mark N. Wegman. Universal classes of hash functions. J. Computer and System Sciences 18(2):143–154, 1979. [Introduced universal and strongly universal hashing, and reintroduced tabulation hashing. Proved that 3-universal hash functions can be composed using bitwise exclusive-or: If h₀, h₁, ..., hᵣ are independent and strongly 3-universal, then H(x₀, x₁, ..., xᵣ) = h₀(a₀) ⊕ h₁(x₁) ⊕ ... ⊕ hᵣ(xᵣ) is also strongly 3-universal.]
Jeffrey Cohen* and Daniel M. Kane*. Bounds on the independence required for cuckoo hashing. Manuscript, 2009. [Cuckoo hashing requires at least 6-independent hash functions.]
Martin Dietzfelbinger and Philipp Woelfel. Almost random graphs with simple hash functions. Proc. 35th Annual ACM Symposium on Theory of Computing 629–638, 2003.
Anna Östlin Pagh and Rasmus Pagh. Uniform hashing in constant time and optimal space. SIAM J. Computing 38(1):85–96, 2008. [Efficient uniform hashing for any fixed set of items.]
Anna Pagh, Rasmus Pagh, and Milan Ružić*. Linear probing with constant independence. SIAM J. Computing 39(3):1107–1120, 2009. [Hashing with linear probing takes Ω(log n) expected worst-case time for pairwise independent hash functions, but O(1) expected worst-case time with 5-independent hash functions.]
Mihai Pătraşcu and Mikkel Thorup. On the k-independence required by linear probing and minwise independence. Proc. 37th International Colloquium on Automata, Languages, and Programming 715–726. Lecture Notes in Computer Science 6198, Springer, 2010. [Hashing with linear probing in O(1) expected worst-case requires 5-independent hash functions.]
Mihai Pătraşcu and Mikkel Thorup. The power of simple tabulation hashing. J. ACM 59(3), article 14, 2012. ArXiv:1011.5200. [Proves that the tabulation-based hash function of Wegman and Carter actually works for cuckoo hashing, despite having only limited independence, when m = Ω(n^{1+ε}).]
Mihai Pătraşcu and Mikkel Thorup. Twisted tabulation hashing. Proc. 24th Annual ACM-SIAM Symposium on Discrete Algorithms, 209–228, 2013. [Adding a second-order tabulation lookup gives much stronger concentration bounds.]
Alan Siegel. On universal classes of extremely random constant-time hash functions. SIAM J. Computing 33:505–543, 2004. [Describes the first algorithms for high-independence hashing in constant time. Also describes tradeoffs between evaluation time and storage space for high-independence hash functions.]
Alan Siegel and Jeanette P. Schmidt. Closed hashing is computable and optimally randomizable with universal hash functions. Technical Report TR1995-687, New York University, April 1995. [Hashing with linear probing takes O(1) expected worst-case time with O(log n)-independent hash functions.]
Mikkel Thorup. Fast and powerful hashing using tabulation. Preprint, May 2015. arXiv:1505.01523. [A survey of recent tabulation-hashing results by Throup and others.]
Mikkel Thorup. String hashing for linear probing. Proc. 20th Annual ACM-SIAM Symposium on Discrete Algorithms, 655–664, 2009.
Mikkel Thorup and Yin Zhang. Tabulation based 4-universal hashing with applications to second moment estimation. Proc. 15th ACM/SIAM Symposium on Discrete Algorithms 615–624, 2004. [Proves that the composite hash function H(x,y) := h(x) ⊕ h'(y) ⊕ h''(x+y) is 4-universal if the component hash functions h, h', h'' are independent and 4-universal.]
Mikkel Thorup and Yin Zhang. Tabulation based 5-universal hashing and linear probing. SIAM J. Computing 41(2):293–331, 2012. [Proves that the composite hash function H(x,y) := h(x) ⊕ h'(y) ⊕ h''(x+y) is 5-universal if the component hash functions h, h', h'' are independent and 5-universal.]
Mark N. Wegman and J. Lawrence Carter. New classes and applications of hash functions. J. Computer and System Sciences 22(3):265–279, 1981. [Degree-(k-1) polynomials over any finite field can be used for strongly k-universal hashing.]
Albert L. Zobrist. A new hashing method with application for game playing. Technical Report 88, Computer Sciences Department, University of Wisconsin, Madison, 1969. [Introduced tabulation hashing.]

Wed Oct 14 Fri Oct 16

No class this week; Jeff was at Oberwolfach.

Wed Oct 21

Bloom filters: basic construction, false positive probability, counting (to support deletions), Bloomier filters

References (click to show/hide)

The output of a (lower-case) bloom filter.

Burton H. Bloom. Space/time trade-offs in hash coding with allowable errors. Communications of the ACM 13(7):422–426, 1970.
Prosenjit Bose, Hua Guo, Evangelos Kranakis, Anil Maheshwari, Pat Morin, Jason Morrison, Michiel Smid, and Yihui Tang. On the false-positive rate of Bloom filters. Information Processing Letters 108(4):210–213, 2008.
Andrei Broder and Michael Mitzenmacher. Network applications of Bloom filters: A survey. Internet Mathematics 1(1):485–509, 2005.
Bernard Chazelle, Joe Kilian, Ronitt Rubinfeld, and Ayellet Tal. The Bloomier filter: an efficient data structure for static support lookup tables. Proc. 15th Annual ACM-SIAM Symposium on Discrete Algorithms, 30–39, 2004.
Ken Christensen, Allen Roginsky, Miguel Jimenoa. A new analysis of the false positive rate of a Bloom filter. Information Processing Letters 110:944—949, 2010.
David Eppstein and Michael T. Goodrich. Space-efficient straggler identification in round-trip data streams via Newton's identities and invertible Bloom filters. Proc. 10th International Workshop on Algorithms and Data Structures 638–649. Lecture Notes in Computer Science 4619, Springer, 2007.
Li Fan, Pei Cao, Jussara Almeida, and Andrei Broder. Summary cache: A scalable wide-area Web cache sharing protocol. IEEE/ACM Transactions on Networking 8(3):281–293, 2000.
Michael T. Goodrich and Michael Mitzenmacher. Invertible Bloom lookup tables. Proc.49th Allerton Conference on Communication, Control and Computing, 792–799, 2011. ArXiv:1101.2245.
Michael Mitzenmacher. Compressed Bloom filters. IEEE/ACM Transactions on Networking 10(5):604–612, 2002.
Anna Pagh, Rasmus Pagh, and S. Srinivasa Rao. An optimal Bloom filter replacement. Proc. 16th Annual ACM-SIAM Symposium on Discrete Algorithms 823—829, 2005.

Fri Oct 23

Locality-sensitive hashing

References (click to show/hide)

Periodically covering the plane with balls.
Andoni and Indyk [CACM 2008]

Alexandr Andoni*, Mayur Datar, Nicole Immorlica, Piotr Indyk, and Vahab Mirrokni. Locality-sensitive hashing scheme based on p-stable distributions. Nearest Neighbor Methods in Learning and Vision: Theory and Practice, 61–72. Gregory Shakhnarovich, Trevor Darrell, and Piotr Indyk, editors, MIT Press, 2006.
Alexandr Andoni* and Piotr Indyk. Near-optimal hashing algorithms for approximate nearest neighbor in high dimensions. Proc. 47th IEEE Symposium on Foundations of Computer Science, 459–468, 2006.
Alexandr Andoni* and Piotr Indyk. Near-optimal hashing algorithms for approximate nearest neighbor in high dimensions. Communications of the ACM 51(1):117–122, 2008.
Alexandr Andoni, Piotr Indyk, Thijs Laarhoven*, Ilya Razenshteyn*, and Ludwig Schmidt*. Practical and aptimal LSH for angular distance. To appear in Proc. 29th Annual Conference on Neural Information Processing Systems, 2015.
Alexandr Andoni and Ilya Razenshteyn*. Optimal data-dependent hashing for approximate near neighbors. Proc. 47th ACM Symposium on Theory of Computing, 2015.
Anirban Dasgupta, Ravi Kumar, and Tamás Sarlós. Fast locality-sensitive hashing. Proc. 17th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 1073–1081, 2011. [Randomized Hadamard transformations instead of random rotations.]
Aristides Gionis*, Piotr Indyk*, and Rajeev Motwani†. Similarity search in high dimensions via hashing. Proc. 25th VLDB Conference, 518–529, 1999.
Piotr Indyk* and and Rajeev Motwani†. Approximate nearest neighbors: towards removing the curve of dimensionality. Proc. 30th Annual ACM Symposium on Theory of Computing 604–613, 1998.
Sariel Har-Peled, Piotr Indyk*, and Rajeev Motwani†. Approximate nearest neighbors: towards removing the curve of dimensionality. Theory of Computing 8:321–350, 2012.
Sariel Har-Peled. A replacement for Voronoi diagrams of near linear size. Proc. 42nd IEEE Symposium on Foundations of Computer Science 94–103, 2001.
Piotr Indyk* and Rajeev Motwani†, Prabhakar Raghavan, and Santosh Vempala*. Locality-preserving hashing in multidimensional spaces. Proc. 29th Annual ACM Symposium on Theory of Computing 618–625, 1997.
Adam Kirsch* and Michael Mitzenmacher. Distance-sensitive Bloom filters. Proc. 8th Workshop Algorithm Engineering and Experiments, 41–50, 2006. [Combines locality sensitive hashing with Bloom filters.]
Nathan Linial and Ori Sasson*. Non-expansive hashing. Combinatorica 18(1):121–133, 1998.

Fun with Bits

Mon Oct 26

Unrealistic integer RAMs: Solving anything in #PSPACE in polynomial time and exponential space (sic)

References (click to show/hide)

Bit masks used to solve QBF in polynomial time, on a unit-cost RAM with multiplication.

Bit. Hacker.

Alberto Bertoni, Giancarlo Mauri, Nicoletta Sabadini. A characterization of the class of functions computable in polynomial time on Random Access Machines. Proc. 13th Annual ACM Symposium on Theory of Computing 168–176, 1981.
Alberto Bertoni, Giancarlo Mauri, Nicoletta Sabadini. Simulations among classes of random access machines and equivalence among numbers succinctly represented. Annals of Discrete Mathematics 25:65–90, 1985.
Michael Brand. Computing with and without arbitrary large numbers. Proc. 10th International Conference on Theory and Applications of Models of Computation, 182--192, 2013. [The unit-cost integer RAM with addition, subtraction, exact division (defined only when the result is an integer), left shift, booleans, and comparisons can compute in polynomial time any function computable on a Turing machine in time bounded by 2⇑n^O(1), where 2⇑k means an exponential twoer of 2's of height k.]
Stephen A. Cook and Robert A. Reckhow. Time bounded random-access machines. Journal of Computer and Systems Sciences 7:354–375, 1973. []
Peter van Emde Boas. Machine models and simulations. Handbook of Theoretical Computer Science, Volume A: Algorithms and Complexity, 1–66. Jan van Leeuwen, editor, MIT Press, 1990.
Juris Hartmanis and Janos Simon. On the power of multiplication in random access machines. 15th Annual IEEE Symposium on Switching and Automata Theory 13–23, 1974.
Vaughan R. Pratt, Michael O. Rabin, and Larry J. Stockmeyer. A characterization of the power of vector machines. Proc. 6th Annual ACM Symposium on Theory of Computing 122–134, 1974.
Arnold Schönhage. On the power of Random Access Machines. Proc. 6th International Colloqiuum on Automata, Languages, and Programming 520--529, 1979.
Janos Simon. Division in idealized unit cost RAMs. J. Computer and System Sciences 22(3):421–441, 1981. [The unit-cost integer RAM with addition, subtraction, exact division (defined only when the result is an integer), left shift, booleans, and comparisons can compute in polynomial time any fucntion computable on a Turing machine in elementary time. Corrected by Brand 2013.]
Janos Simon and Mario Szegedy. On the complexity of RAM with various operation sets. Proc. 24th Annual ACM Symposium on Theory of Computing, 624–631, 1992.

Wed Oct 28 Fri Oct 30

Realistic integer RAMs: transdichotomous RAM, word RAM, AC⁰ RAM
Ordered dictionaries: van Emde Boas trees, x-fast tries, y-fast tries via indirection, fusion trees, exponential search trees

References (click to show/hide)

Predecessor search over a finite universe
[Mihai Pătraşcu]

Part of a exponential tree, with the root on the left and children on the right
[Andersson Thorup 2007]

Arne Andersson. Faster deterministic sorting and searching in linear space. Proc. 37th Annual IEEE Symposium on Foundations of Computer Science 135–141, 1996. [Dynamic ordered dictionary with O(√log n) query and amortized update time using O(n) space, for any word size w, via exponential trees.]
Rene De La Briandais. File searching using variable length keys. 1959 Proc. Western Joint Computer Conference, 295–298, 1959. [Describes a tree data structure similar to tries, but with (sparse) high-degree nodes represented by linked lists.]
Arne Andersson, Peter Bro Miltersen, and Mikkel Thorup. Fusion trees can be implemented with AC⁰ instructions only. Theoretical Computer Science 215(1-2):337-344, 1999. [...but they may require AC⁰ instructions that are not standard C operations.]
Arne Andersson and Mikkel Thorup. Dynamic ordered sets with exponential search trees. J. ACM 54(3), article 13, 2007. [Combined journal version of Andersson's FOCS 1996 paper and Andersson and Thorup's STOC 2000 paper.]
Arne Andersson and Mikkel Thorup. Tight(er) worst-case bounds on dynamic searching and priority queues. Proc. 32nd Annual ACM Symposium on Theory of Computing, 335–342, 2000. [Dynamic ordered dictionary with with optimal worst-case update and query time O(sqrt(log n/log log n)), using O(n) space, for any word size w, using only C instructions (including multiplication), via worst-case efficient exponential trees.]
Paul Beame and Faith E. Fich. Optimal bounds for the predecessor problem and related problems. J. Computer and System Sciences 65(1):38–72, 2002. [Dynamic ordered dictionary with optimal query and amortized update time O(min{log w/log log w, sqrt(log n/log log n)}), using Andersson's exponential search trees, as well as matching cell-probe lower bounds. The paper includes an impressively thorough survey of previous upper and lower bounds for ordered dictionaries and several related data structure problems.]
Peter van Emde Boas. An O(n log log n) on-line algorithm for the Insert-Extract Min problem. Technical Report TR 74-221, Computer Science Department, Cornell University, December 1974. [The original version of “stratified trees”, which required O(u log log u) space.]
Peter van Emde Boas. Preserving order in a forest in less than logarithmic time. 16th Annual IEEE Symposium on Foundations of Computer Science 75–84, 1975. [An updated version of “stratified trees” that uses only O(u) space, by way of indirection. Apparently the idea of separately storing the min and max element of every chunk was developed later.]
Peter van Emde Boas, R. Kaas, and E. Zijlstra. Design and implementation of an efficient priority queue. Mathematical Systems Theory 10:99–127, 1977. [The first formal publication of the original version of “stratified trees”, which required O(u log log u) space. I never knew that the up-tree data structure for disjoint sets was called a ”Tritter tree“!]
Edward Fredkin. Trie memory. Communications of the ACM 3:490–499, 1962. [Fredkin pronounced it “tree”, as in ”retrieval”.]
Michael L. Fredman and Dan E. Willard. BLASTING through the information theoretic barrier with FUSION TREES. Proc. 22nd Annual ACM Symposium on Theory of Computing 1-7, 1990. [The conference version of the original fusion tree paper. Dynamic ordered dictionary with O(log n/log w) query and (amortized) update time using O(n) space. If you cite this paper, please use the proper capitalization and sizing; thank you.]
Michael L. Fredman and Dan E. Willard. Surpassing the information theoretic bound with fusion trees. J. Computer and System Sciences 47(3):424-436, 1993. [The journal version of the original fusion tree paper. Apparently the referees did not have a sense of humor.]
Michael L. Fredman and Dan E. Willard. Trans-dichotomous algorithms for minimum spanning trees and shortest paths. J. Computer and System Sciences 48:533–551, 1994.
Mihai Pătraşcu and Mikkel Thorup. Time-space trade-offs for predecessor search. Proc. 38th Annual ACM Symposium on Theory of Computing, 232–240, 2006.
Mihai Pătraşcu and Mikkel Thorup. Randomization does not help searching predecessors. Proc. 18th Annual ACM/SIAM Symposium on Discrete Algorithms 555–564, 2007. [Tight cell-probe lower bounds for static ordered dictionaries, for any number of integers with any number of bits each, any word size, and any space bound.]
Dan E. Willard. Log-logarithmic worst case range queries are possible in space O(N). Information Processing Letters 17(2):81–89, 1983. [x-fast tries and y-fast tries: queries in O(log w) time using O(n) space. The paper only describes the static data structure, because dynamic perfect hash tables were not yet known.]
Dan E. Willard. New trie data structures which support very fast search operations. J. Computer and System Sciences 28:379–394, 1984. [p-fast tries and q-fast tries: both queries and updates in O(sqrt{w}) time using O(n) space.]

Wed Nov 4

Fast integer sorting: radix sort, packed sorting, Batcher's bitonic parallel mergesort, signature sort

References (click to show/hide)

Sorting a stack of Indecks notched cards.
From The Last Whole Earth Catalog (1975)

Diagram for Combination Counting
[Hollerith 1890]

A McBee Keysort card.
[Anderson 1949]

Representing 94, without and with a Single Figure notch.
[Anderson 1949]

Susanne Albers and Torben Hagerup. Improved parallel integer sorting without concurrent writing. Information and Computation 136(1):25–51, 1997. [Packed sorting: Sorts n b-bit integers in O(n) time, using word size w = Ω(b log n log log n]
Arne Andersson, Torben Hagerup, Stefan Nilsson*. Blasting past fusion trees. Technical Report LU-CS-TR:94-135, Department of Computer Science, Lund University, 1994. [O(n log log n) time for all w≥log n. Requires hashing (and therefore randomization) to work in only O(n) space. See also Han and Shen 1995.]
Arne Andersson, Torben Hagerup, Stefan Nilsson*, and Rajeev Raman. Sorting in linear time? J. Computer and System Sciences 57(1):74–93, 1998. [Signature Sort: O(n) expected time for all w ≥ Ω(log^{2+ε} n), using a "full instruction set". Also: O(n log log n) time for all w, using a restricted instruction set (and hashing to get O(n) space).]
Kenneth E. Batcher. Bitonic sorting. Goodyear Aerospace Report GER-11869, 1964. [Batcher got his PhD from UIUC in 1964!]
Kenneth E. Batcher. Sorting networks and their applications. Proc. AFIPS Spring Joint Computer Conference, Vol. 32, 307–314, 1968. [Bitonic and even-odd sorting networks. Bitonic mergesort is a key component in Albers and Hagerup's packed sorting algorithm. Batcher got his PhD from UIUC in 1964!]
Amir M. Ben-Amram* and Zvi Galil. When can we sort in o(n log n) time? J. Computer and System Sciences 54:345–370, 1997. [If and only if (1) either w is not enormous or we allow nonuniform algorithms, and (2) either memory is huge or we allow double-precision multiplication.]
Leslie J. Comrie. The Hollerith and Powers tabulating machines. Transactions of the Office Machinery Users' Association, 25–37, 1929–30. [Possibly the first published description of radix sort. Comrie was the first person to use punched-card equipment for scientific (rather than business and statistical) purposes.]
Yijie Han. Fast integer sorting in linear space. Proc. 17th Annual Symposium on Theoretical Aspects of Computer Science, 242–253. Lecture Notes in Computer Science 1770, Springer, 2000. [O(n (log log n)^{3/2}) time, without hashing.]
Yijie Han. Improved fast integer sorting in linear space. Proc. 12th Annual ACM-SIAM Symposium on Discrete Algorithms, 793–796, 2001. [O(n log log n log log log n) time for all w, and O(n log log n) for all w ≥ Ω(log^{2+ε} n), without hashing.]
Yijie Han. Deterministic sorting in O(n log log n) time and linear space. J. Algorithms 50(1):96–105, 2004. [Avoids hashing.]
Yijie Han and Xiaojun Shen. Conservative algorithms for parallel and sequential integer sorting. Proc. 1995 International Computing and Combinatorics Conference, 324–333. Lecture Notes in Computer Science 959, Springer, 1995. [O(n log log n) time for all w≥log n. Requires hashing (and therefore randomization) to work in only O(n) space. See also Andersson, Nilsson, and Hagerup 1994.]
Yijie Han and Mikkel Thorup. Integer sorting in O(n √log log n) expected time and linear space. Proc. 43rd Symposium on Foundations of Computer Science, 135–144, 2002.
Herman Hollerith. Complete specification: Improvements in the methods of and apparatus for compiling statistics. UK Patent № 327, January 8, 1889. [Includes a description of multi-key sorting, using an algorithm similar to radix sort. “The most complicated combinations can readily be counted with comparatively few counters or relays by first assorting the cards according to the first items entering into the combinations, then re-sorting each group according to the second item entering into the combination, and so on, and finally counting on a few counters the last item of the combinations for each group of cards.“]
David G. Kirkpatrick and Stefan Reisch*. Upper bounds for sorting integers on random access machines. Theoretical Computer Science 28(3):263–276, 1984. [How to sort n integers in O(n log(w/log n)) time on a w-bit word RAM, or in O(n) time on an abstract integer RAM.]
Stefan Nilsson*. Radix Sorting & Searching. PhD thesis, Department of Computer Science, Lund University, 1996.
Stefan Nilsson. The fastest sorting algorithm? Dr. Dobb's Journal 311:38–45, 2000. [Includes C source code for Signature Sort.]
Mikkel Thorup. Randomized sorting in O(n log n) time and linear space using addition, shift, and bit-wise boolean operations. J. Algorithms, 42(2):205–230, 2002.
Dan E. Willard. Log-logarithmic worst case range queries are possible in space O(N). Information Processing Letters 17(2):81–89, 1983. [How to sort n integers in O(n log w) time, via y-fast tries.]

Fri Nov 6

Priority queues: atomic heaps, equivalence with sorting, black-box O(1)-time insertion, black-box melding

References (click to show/hide)

A triage tag.
[See also]

Miklós Ajtai, Michael L. Fredman, and János Komlós. Hash functions for priority queues. Information and Control 63(3):217–225, 1984. [Θ(w^{n-1}) space is necessary and sufficient for O(1)-time priority queues via hashing.]
Stephen Alstrup, Thore Husfeldt, Theis Rauhe, and Mikkel Thorup. Black box for constant-time insertion in priority queues. ACM Transactions on Algorithms 1(1):102–106, 2005. [Any priority queue that supports INSERT, DELETE, and FINDMIN in t(n) time can be transformed into a priority queue that supports INSERT and FINDMIN in O(1) time and DELETE in O(t(n)) time.]
Arne Andersson and Mikkel Thorup. Dynamic ordered sets with exponential search trees. J. ACM 54(3), article 13, 2007. [Exponential trees: A sorting algorithm that runs in nS(n) time can be used as a black box to implement a priority queue supporting all operations in O(S(n) log log n) time.]
Peter van Emde Boas, R. Kaas, and E. Zijlstra. Design and implementation of an efficient priority queue. Mathematical Systems Theory 10:99–127, 1977. [Any priority queue that supports INSERT, DELETE, and FINDMIN in t(n) amortized time can be modified to support INSERT, DELETE, FINDMIN, and MELD in O(t(n)α(n)) amortized time, where α(n) is the inverse Ackermann function. The new meldable priority queue is a union-find structure whose nodes are black-box non-meldable priority queues.]
Michael L. Fredman and Dan E. Willard. Surpassing the information theoretic bound with fusion trees. J. Computer and System Sciences 47(3):424-436, 1993. [Atomic heaps: maintain O(log²n) items in O(1) time per operation. The main component of fusion trees and AF-heaps.]
Michael L. Fredman and Dan E. Willard. Trans-dichotomous algorithms for minimum spanning trees and shortest paths. Proc. 31st Annual IEEE Symposium on Foundations of Computer Science 719–725, 1990. [Minimum spanning trees in O(m) time via atomic heaps. Dijkstra's shortest path algorithm in O(m + n log n/log log n) time via atomic Fibonacci heaps.]
Ran Mendelson*, Robert E. Tarjan, Mikkel Thorup, and Uri Zwick. Melding priority queues. ACM Transactions on Algorithms 2(4):535–556, 2006. [Improves the analysis of van Emde Boas, Kass, and Zijlstra's priority queue reduction. Any priority queue that supports INSERT, DELETE, and FINDMIN in t(n) amortized time can be modified to support INSERT, FINDMIN, and MELD in O(1) amortized time, and DELETE in O(t(n) + α(n)) amortized time, where α(n) is the inverse Ackermann function.]
Mikkel Thorup. Equivalence between priority queues and sorting. J. ACM 54(6), article 28, 2007. [A sorting algorithm that runs in nS(n) time can be used as a black box to implement a priority queue that supports INSERT and DELETEin O(S(n)) time and FINDMIN in O(1) time, on an integer RAM with multiplication. (The reverse reduction is trivial.) The results are slightly weaker for AC⁰ RAMs.]

Not this semester :-(

Least common ancestors: reduction from range minimum queries, reduction to ±1 range minimum queries, induction, the four-Russians trick, heavy-light tree decomposition (again), alphabetic coding, longest common prefix (again), rake-compress trees (again)

References (click to show/hide)

A phylogeny of Christian churches reconstructed from memetic analysis (with the Episcopalian meme given a weight of 8)
[Lord and Price 2001]

Alfred V. Aho, John E. Hopcroft, and Jeffrey D. Ullman. On finding lowest common ancestors in trees. SIAM J. Computing 5(1):115–132, 1976.
Stephen Alstrup, Cyril Gavoille, Haim Kaplan, and Theis Rauhe. Nearest common ancestors: A survey and a new algorithm for a distributed environment. Theory of Computing Systems 37(3):441–456, 2004.
Michael A. Bender and Martin Farach-Colton. The LCA problem revisited. Proc. 4th Latin American Symposium on Theoretical Informatics, 88–94. Lecture Notes in Computer Science 1776, Springer, 2000.
Michael A. Bender and Martin Farach-Colton. The level-ancestor problem simplified. Theoretical Computer Science 321(1):5–12, 2004.
Omer Berkman*, Dany Breslauer*, Zvi Galil, Baruch Schieber*, and Uzi Vishkin. Highly parallelizable problems. Proc. 21st Annual ACM Symposium on Theory of Computing, 309–319, 1989.
Omer Berkman* and Uzi Vishkin. Recursive star-tree parallel data structure. SIAM J. Computing 22(2):221–242, 1993.
Johannes Fischer. Optimal succinctness for range minimum queries. Proc. 9th Latin American Symposium on Theoretical Informatics, 158–169. Lecture Notes in Computer Science 6034, Springer, 2010.
Johannes Fischer* and Volker Heun. Theoretical and practical improvements on the RMQ-problem, with applications to LCA and LCE. Proc. 17th Annual Symposium on Combinatorial Pattern Matching, 36–48. Lecture Notes in Computer Science 4009, Springer, 2006.
Johannes Fischer and Volker Heun. Space-efficient preprocessing schemes for range minimum queries on static arrays. To appear in SIAM J. Computing, 2011.
Dov Harel*. A linear time algorithm for the lowest common ancestors problem (extended abstract). Proc. 21st Annual IEEE Symposium on Foundations of Computer Science, 308–319, 1980.
Dov Harel* and Robert E. Tarjan. Fast algorithms for finding nearest common ancestors. SIAM J. Computing 13(2):338–355, 1984.
Harold N. Gabow, Jon Louis Bentley, and Robert E. Tarjan. Scaling and related techniques for geometry problems". Proc. 16th ACM Symposium on Theory of Computing 135–143, 1984.
Baruch Schieber* and Uzi Vishkin. On finding lowest common ancestors: Simplification and parallelization. SIAM J. Computing 17(6):1253–1262, 1988.

Wed Nov 11

No class today; Jeff was at Princeton.

Fri Nov 13

Overview of project proposals

Fun with Time

Wed Nov 18

Partial persistence: fat nodes, path copying, node copying, fractional cascading, planar point location

References (click to show/hide)

A persistent hash map (via path copying) in Clojure
[Hickey 2008]

Fractional cascading, illustrated by Jorge Stolfi
[Chazelle Guibas 1986]

Ali R. Boroujerdi and Bernard M. E. Moret. Persistent linked structures at constant worst-case cost. Proc. 8th International Conference on Computing and Information, 68-78, 1996.
Gerth Stølting Brodal*. Partially persistent data structures of bounded degree with constant update time. Nordic J. Computing 3(3):238–255, 1996.
Bernard Chazelle and Leonidas J. Guibas. Fractional cascading: I. A data structuring technique. Algorithmica 1(1):133–162, 1986.
Bernard Chazelle and Leonidas J. Guibas. Fractional cascading: II. Applications. Algorithmica 1(1):163–191, 1986.
David P. Dobkin and J. Ian Munro. Efficient uses of the past. Proc. 21st Annual IEEE Symposium on Foundations of Computer Science, 200-206, 1980.
James R. Driscoll, Neil Sarnak*, Daniel D. Sleator, and Robert E. Tarjan. Making data structures persistent. J. Computer and System Sciences 38(1):86–124, 1989.
Christopher W. Fraser and Eugene W. Myers. An editor for revision control. ACM Transactions on Programming Languages and Systems 9(2):277–295, 1987.
Timo J. G. Krijnen and Lambert Meertens. Making B-trees work for B. Mathematical Centre Report IW 219, Mathematisch Centrum, Amsterdam, 1983.
Marc H. Overmars*. Searching in the past I. Technical Report RUU-CS-81-9, Department of Computer Science, University of Utrecht, 1981.
Marc H. Overmars*. Searching in the past II: General transforms. Technical Report RUU-CS-81-9, Department of Computer Science, University of Utrecht, 1981.
Neil Sarnak* and Robert E. Tarjan. Planar point location using persistent search trees. Communications of the ACM 29(7):669–679, 1986.

Fri Nov 20

Full persistence: Euler tours, ordered list maintenance, virtual scapegoat trees

References (click to show/hide)

A Final Thought
[Bender et al. 2002]

AVL dags and version trees
[Fraser and Myers 1987]

Arne Andersson. General balanced trees. J. Algorithms 30:1–28, 1999. [The rebalancing algorithm for scapegoat trees is almost identical to the tag relabeling algorithm of Bender et al., including the analysis. Both algorithms redistribute keys in an unbalanced interval as evenly as possible, so that there are exactly two gap sizes. The only difference between the algorithms is that in the tag relabeling algorithm, the two gap sizes are consecutive integers, but using scapegoat trees, the two gap sizes are consecutive powers of 2.]
Michael A. Bender, Richard Cole, Erik D. Demaine, Martin Farach-Colton, and Jack Zito*. Two simplified algorithms for maintaining order in a list. Proc. 10th Annual European Symposium on Algorithms, 152–164. Lecture Notes in Computer Science 2461, Springer, 2002.
Paul F. Dietz. Maintaining order in a linked list. Proc. 14th Annual ACM Symposium on Theory of Computing, 122–127, 1982.
Paul F. Dietz and Daniel D. Sleator. Two algorithms for maintaining order in a list. Proc. 19th Annual ACM symposium on Theory of Computing, 365–372, 1987.
Christopher W. Fraser and Eugene W. Myers. An editor for revision control. ACM Transactions on Programming Languages and Systems 9(2):277–295, 1987.
Athanasios K. Tsakalidis. Maintaining order in a generalized linked list. Acta Informatica 21(1):101–112, 1984.

Confluent persistence: Hand, hand, fingers, thumb. Dum ditty, dum ditty, dum dum dum.

References (click to show/hide)

Replacing the preﬁx of a pedigree in the compressed path method.
[Fiat Kaplan 2000]

Fingers, prosthetic ﬁngers, tendons, knuckles, and the hand.
[Demaine et al. 2010]

Jim Apple [jbapple] and others. What's new in purely functional data structures since Okasaki? Theoretical Computer Science – Stack Exchange, January 2011.
Adam L. Buchsbaum and Robert E. Tarjan. Confluently persistant deques via data structural bootstrapping. J. Algorithms 18:513–547, 1995.
Erik D. Demaine, Stefan Langerman, and Eric Price*. Confluently persistent tries for efficient version control. Algorithmica 57(3):462–483, 2010.
James R. Driscoll, Daniel D. K. Sleator, and Robert E. Tarjan. Fully persistent lists with catenation. J. ACM 41(5): 943–959, 1994.
Amos Fiat and Haim Kaplan. Making data structures confluently persistent. J. Algorithms 48:16–38, 2000.
Gerard Huet. Functional pearl: The zipper. J. Functional Programming 7(5):549-554, 1997.
Haim Kaplan, Chris Okasaki, and Robert E. Tarjan. Simple confluently persistent catenable lists. SIAM J. Computing 30(3):965-977, 2000.
Haim Kaplan and Robert E. Tarjan. Purely functional, real-time deques with catenation. J. ACM 46(5):577–603, 1999.
Chris Okasaki*. Amortization, lazy evaluation, and persistence: Lists with catenation via lazy linking. Proc. 36th Annual IEEE Symposium on Foundations of Computer Science, 646–654, 1995.
Chris Okasaki. Purely Functional Data Structures. Cambridge University Press, 1998.
Chris Okasaki*. Purely Functional Data Structures. Ph.D. thesis, School of Computer Science, Carnegie Mellon University, September 1996.
Chris Okasaki*. The role of lazy evaluation in amortized data structures. SIGPLAN Notices 31(6), 62–72, 1996.
They Might Be Giants. Fingertips. Apollo 18, 1992.
The Residents. Fingertips. The Commercial Album, 1980.
Stevie Wonder*. Fingertips. The 12-Year-Old Genius, 1963.

Not this semester :-(

Retroactive data structures: changing the past, rollback, lower bounds via polynomial evaluation, retroactive priority queues via bridges, partial to full retroactivity via √m checkpoints

References (click to show/hide)

Primer timelines [SPOILER!]

Retroactively inserting insertions.
[Demaine et al. 2007]

“You're about to have an idea for a time machine.”
“I am?”

Primer timelines [SPOILER!]

Umut A. Acar, Guy E. Blelloch, and Kanat Tangwongsan*. Non-oblivious retroactive data structures. Technical Report CMU-CS-07-169, Carnegie Mellon University, December 11, 2007. [A variant of retroactive data structures in which revisions inform the user about changes to past queries.]
Umut A. Acar, Guy E. Blelloch, Ruy Ley-Wild*, Kanat Tangwongsan*, and Duru Türkoğlu*. Traceable data types for self-adjusting computation. Proc. 2010 ACM SIGPLAN Conference on Programming Language Design and Implementation, 483–496, 2010. [A variant of retroactive data structures that maintains a list of queries as well as updates; any revision returns a pointer to the earliest query whose answer is changed by the revision.]
Guy E. Blelloch. Space-efficient dynamic orthogonal point location, segment intersection, and range reporting. Proc. 19th Annual ACM-SIAM Symposium on Discrete Algorithms, 894–903, 2008. [Fully dynamic retroactive ordered dictionaries with O(log n) amortized retroactive query and revision time.]
Erik D. Demaine, John Iacono, and Stefan Langerman. Retroactive data structures. ACM Transactions on Algorithms 3(2), article 13, 2007. [Introduced retroactive data structures.]
Matthew T. Dickerson, David Eppstein, and Michael T. Goodrich. Cloning Voronoi diagrams via retroactive data structures. Proc. 18th Annual European Symposium on Algorithms, 362–373. Lecture Notes in Computer Science 6346, Springer, 2010.
Yoav Giora* and Haim Kaplan. Optimal dynamic vertical ray shooting in rectilinear planar subdivisions. ACM Transactions on Algorithms 5(3), article 28, 2009. [Journal version of the following paper. Yes, the first author's name is spelled correctly.]
Yoav Giyora* and Haim Kaplan. Optimal dynamic vertical ray shooting in rectilinear planar subdivisions. Proc. 18th Annual ACM-SIAM Symposium on Discrete Algorithms, 19–28, 2007. [Fully dynamic retroactive ordered dictionaries with O(log n) worst-case retroactive query and revision time. The time bound is optimal in the comparison model, but the data structure requires the word-RAM model internally. Yes, the first author's name is spelled correctly.]
Yakov Nekrich. Searching in dynamic catalogs on a tree. Preprint, July 2010. ArXiv:1007.3415. [Fully dynamic retroactive ordered dictionaries with O(log n/log log n) retroactive update time, which is optimal in the cell probe model by reduction from the marked ancestor problem.]

Wed Nov 25 Fri Nov 27

Thanksgiving break: No class this week

Fun with Big Data

Wed Dec 2

An obsolete tape robot at Fermi National Lab; each tape cartridge holds about a terabyte.

A modern tape robot

External-memory data structures: basic definitions and parameters (N, M, and B), fundamental upper and lower bounds (scan, sort, permute, and search), B-trees, sub-constant-time updates via buffering

Alok Aggarwal and Jeffrey Scott Vitter. The input/output complexity of sorting and related problems. Communications of the ACM 31(9):1116–1127, 1988. [Introduces the formal external-memory model; proves that sorting requires sort(N) := Θ(n log_m n) I/Os and permuting requires Θ(min{N, n log_m n}) I/Os; describes optimal external-memory versions of mergesort and quicksort.]
Lars Arge*. The buffer tree: A technique for designing batched external data structures. Algorithmica 37:1-24, 2003.
Lars Arge, Andrew Danner*, and Sha-Mayn Teh*. I/O-efficient point location using persistent B-trees. J. Experimental Algorithmics 8, article 2.1, 2003. [Describes subtle but important changes to persistent B-trees making them useful for point location.]
Lars Arge and Jeffrey Scott Vitter. Optimal external memory interval management. SIAM J. Computing 32(6):1488–1508, 2003. [Weight-balanced B-trees.]
Rudolf Bayer and Edward M. McCreight. Organization and maintenance of large ordered indexes Acta Informatica 1(3):173–189, 1972. [The first B-tree paper.]
Bruno Becker, Stephan Gschwind, Thomas Ohler, Bernhard Seeger, and Peter Widmayer. An asymptotically optimal multiversion B-tree. VLDB Journal 5(4):264–275, 1996. [Describes an external-memory version of the partial persistence via node-splitting, and develops an efficient partially persistent B-tree.]
Jeff Erickson. Lower bounds for external algebraic decision trees. Proc. 16th Annual ACM-SIAM Symposium on Discrete Algorithms, 755–761, 2005.
Ramzi Fadel*, Kim Vagn Jakobsen*, Jyrki Katajainen, and Jukka Teuhola. Heaps and heapsort on secondary storage. Theoretical Computer Science 220(2):345–362, 1999. [Uses buffer tree to implement an optimal external-memory version of heapsort.]
Michael T. Goodrich, Jyh-Jong Tsay*, Darren Erik Vengroff*, and Jeffrey Scott Vitter. External-memory computational geometry. Proc. 34th Annual IEEE Symposium on Foundations of Computer Science, 714–723, 1993.
Scott Huddleston and Kurt Mehlhorn. A new data structure for representing sorted lists. Acta Informatica 17:157–184, 1982. [Introduced (a,b)-trees.]
Rasmus Pagh. Basic external memory data structures. Algorithms for Memory Hierarchies: Advanced Lectures, 14–35. Ulrich Meyer, Peter Sanders, and Jop F. Sibeyn, editors. Lecture Notes in Computer Science 2625, Springer, 2003.
Peter Sanders. Memory Hierarchies—Models and Lower Bounds. Algorithms for Memory Hierarchies: Advanced Lectures, 1–13. Ulrich Meyer, Peter Sanders, and Jop F. Sibeyn, editors. Lecture Notes in Computer Science 2625, Springer, 2003.
Jeffrey Scott Vitter. Algorithms and data structures for external memory. Foundations and Trends® in Theoretical Computer Science 2(4), 305–474, 2006. [A recent extensive survey. Yes, the journal name includes a registered-trademark symbol.]

Fri Dec 4

Answering a 3-sided query: One node in an external-memory priority search tree
[Agarwal et al. 2002]

Answering a 3-sided query: Inside the catalog structure
[Agarwal et al. 2002]

External-memory range searching: external-memory interval trees; external-memory priority search trees; catalog structures for O(B²) points/intervals; external-memory range trees.

Pankaj K. Agarwal, Lars Arge, and Jeff Erickson. Indexing moving points. J. Computer and System Sciences 66:207-243, 2003. [Persistent kinetic multilevel external range trees. Whew!]
Lars Arge. External memory geometric data structures. Lecture notes, University of Aarhus, August 2005.
Lars Arge and Jeffrey Scott Vitter. Optimal external memory interval management. SIAM J. Computing 32(6):1488–1508, 2003. [External-memory interval trees.]
Lars Arge, Vasilis Samoladas*, and Jeffrey Scott Vitter. On two-dimensional indexability and optimal range search indexing. Proc. 18th ACM Symposium on Principles of Database Systems 346–357, 1999. [External priority search trees, including the B²-point catalog structure, and external range trees.]
Bernard Chazelle. Lower bounds for orthogonal range searching: I. The reporting case. J. ACM 37(2):200–212, 1990. [Any in-core data structure that stores n points in the plane in S(n) space and answers rectangular range-reporting queries in T(n) + O(k) time must satisfy S(n) log T(n) = Ω(n log n). In particular, if T(n) = O(polylog n), then S(n) = Ω(n log n/log log n). I wish I'd had time to talk about this.]
Herbert Edelsbrunner*. A new approach to rectangle intersections, part I. International J. Computer Mathematics 13:209–219, 1983. [Introduced interval trees, under the name “1-fold rectangle trees”.]
Paris Kanellakis, Sridhar Ramaswamy*, Darren E. Vengroff*, and Jeffrey Scott Vitter. Indexing for data models with constraints and classes. J. Computer and System Sciences 52, 589–612, 1996. [Introduced the first B⊃2-point catalog structure for interval stabbing, which is much more complex than the one in Arge et al. 1999.]
Edward M. McCreight. Priority search trees. SIAM J. Computing 14(2):257–276, 1985.
Sairam Subramanian and Sridhar Ramaswamy. The P-range tree: A new data structure for range searching in secondary memory. Proc. 6th Annual ACM-SIAM Symposium on Discrete Algorithms 378–387, 1995. [Describes a linear-size data structure that answers 3-sided range queries in O(log_Bn + k + log** B) I/Os, which is perhaps the only occurrence of the doubly-iterated logarithm ever seen in the wild. Also proves that answering 4-sided queries in O(polylog_Bn + k) I/Os requires Ω(n log_Bn/log_Blog_Bn) blocks.]

Wed Dec 9

The van Emde Boas layout
[Bender et al. 2000]

A funnel heap
[Brodal Fagerberg 2002]

Cache-oblivious data structures: definitions, tall caches, van Embe Boas layout, exponential layout, funnelsort, funnel heaps, exponential-level priority queues

Lars Arge, Gerth Stølting Brodal, and Rolf Fagerberg. Cache-oblivious data structures. Chapter 34 of Handbook of Data Structures and Applications. Dinesh Mehta and Sartaj Sahni, editors, CRC Press, 2005.
Michael A. Bender, Richard Cole, and Rajeev Raman. Exponential structures for cache-oblivious algorithms. Proc. 29th International Colloquium on Automata, Languages, and Programming, 195–207. Lecture Notes in Computer Science 2380, Springer, 2002.
Michael A. Bender, Erik D. Demaine, and Martin Farach-Colton. Cache-oblivious B-trees. Proc. 41st Annual Symposium on Foundations of Computer Science 399–409, 2000.
Michael A. Bender, Ziyang Duan, John Iacono, and Jing Wu. A locality-preserving cache-oblivious dynamic dictionary. Proc. 13th Annual ACM-SIAM Symposium on Discrete Algorithms 29–38, 2002.
Gerth Stølting Brodal, Erik D. Demaine, Jeremy T. Fineman, John Iacono, Stefan Langerman, and J. Ian Munro. Cache-oblivious dynamic dictionaries with optimal update/query tradeoff. Proc. 21st Annual ACM-SIAM Symposium on Discrete Algorithms 1448–1456, 2010.
Gerth Stølting Brodal and Rolf Fagerberg. Cache oblivious distribution sweeping. Proc. 29th International Col loquium on Automata, Languages, and Programming, 426–438. Lecture Notes in Computer Science 2380, Springer, 2002.
Gerth Stølting Brodal and Rolf Fagerberg. Funnel heap - A cache oblivious priority queue. Proc. 13th Annual International Symposium on Algorithms and Computation 219-228. Lecture Notes in Computer Science 2518, Springer, 2002.
Gerth Stølting Brodal and Rolf Fagerberg. On the limits of cache-obliviousness. Proc. 35th Annual ACM Symposium on Theory of Computing 307–315, 2003.
Gerth Stølting Brodal, Rolf Fagerberg, and Riko Jacob. Cache oblivious search trees via binary trees of small height. Proc. 13th Annual ACM-SIAM Symposium on Discrete Algorithms 39–48, 2002.
Matteo Frigo, Charles E. Leiserson, Harald Prokop*, Sridhar Ramachandran. Cache-oblivious algorithms. Proc. 40th Annual IEEE Symposium on Foundations of Computer Science 285–298, 1999.
Harald Prokop*. Cache-Oblivious Algorithms. Master's Thesis, Dept. Electrical Engineering and Computer Science, Massachusetts Institute of Technology, June 1999.

Fun with Research

Finals week dates TBA

Chicken chicken chicken.
[Zongker 2002, 2006]

QED.
[Vargomax 2007]

Project presentations! — Siebel 4407

Jeremy Stribling*, Daniel Aguayo*, and Maxwell Krohn*. Rooter: A methodology for the typical uniﬁcation of access points and redundancy. Manuscript, accepted to the 9th World Multi-Conference on Systemics, Cybernetics, and Informatics, Orlando, FL, July 2005. [Automatically generated.]
Vargomax V. Vargomax*. Generalized Super Mario Bros. is NP-complete. Proc. 6th Binarennial Workshop about Symposium on Robot Dance Party of Conference in Celebration of Harry Bovik’s (2⁶)ᵗʰ Birthday 87–88, 2007. [ Vargomax's conference presentation is online.]
Doug Zongker*. Chicken chicken chicken: Chicken Chicken. Proc. Preantepenultimate Workshop on Potentially Computer Science, 2002.
Doug Zongker*. Chicken chicken chicken: Chicken Chicken. Ann. Improb. Res. 12(5):16–21, 2006. [Archival journal version of previous paper; identical except for typechicken.]
Жуков Михаил Сергеевич*. Корчеватель: алгоритм типичной унификации точек доступа и избыточности. Журнал научных публикаций аспирантов и докторантов, 2008. [Russian translation of Stribling et al. 2005.]

CS 598 JGE: Advanced Data Structures (Fall 2015)

❖ Announcements ❖ Schedule ❖ Projects ❖

❖ Pointers ❖ Tables ❖ Bits ❖ Time ❖ Big Data ❖ Related Topics ❖

Fun with Pointers

Fun with Tables

Fun with Bits

Fun with Time

Fun with Big Data

Fun with Research

Related Topics

Fun with Pointers

Fun with Bits

Fun with Geometry

Fun with Big Data