Crossing Lemma (Ajtai, Chvátal, Newborn, and Szemerédi; Leighton): Any graph with n vertices and e > 4n edges has crossing number Omega(e3/n2).
Proof (folklore):
Consider a planar embedding of a graph with n vertices, e edges, and
c pairs of crossing edges.
Euler's formula implies
that c > e-3n. Take a random subset of the vertices, each vertex
with probability p. The expected number of vertices, edges, and crossings in the
induced subgraph are at least pn, p2e, and
p4c, respectively. Thus, p4c >
p2e - 3pn, which implies c >
e/p2 - 3n/p3. Taking p =
4n/e gives us
Theorem (Dey): Any set of n points in the plane has at most O(n4/3) halving lines.
Proof (Dey): Assume without loss of generality that n is even. Let S be a set of n points in the plane. Let H be the set of line segments with endpoints p,q in S, such that the line through pq is a halving line.
The segments in H can be decomposed into n/2 convex chains as follows. Start with a vertical line through one of the n/2 leftmost points p in S, and rotate this line clockwise around p until it contains a segment pq in H. Initially, there are less than n/2 points above the line; this number goes down whenever the line hits a point to the left of p, and goes up whenever it hits a point to the right of p. It follows that q must lie to the right of p. Continue rotating the line clockwise around q until it hits another segment in H (which will lie to the right of q), and so on, until the line is vertical again. The sequence of segments hit by the rotating line forms a convex chain, and every segment in H is in exactly one convex chain. (These convex chains are dual to the concave chains studied by Agarwal, Aronov, and Sharir.)
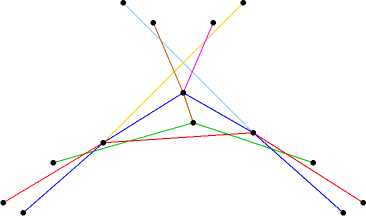
A set of 14 points with 14 halving lines, split into 7 convex chains
The number of intersections between any two convex chains is no more than the number of upper common tangents between the same two chains. Any line between two points in S is an upper common tangent of at most one pair of chains. Thus, there are at most O(n2) intersections between the segments in H. By the Crossing Lemma, any graph with n vertices and crossing number O(n2) has at most O(n4/3) edges, so S has at most O(n4/3) halving lines, QED.
Dey's proof of the O(nk1/3) upper bound on k-sets is almost this simple. The only other result he needs is that the maximum number of <k-sets is n(k-1), which was proved by Alon and Gyõri.
Thanks to Pankaj Agarwal for pointing out a gap in an earlier version of this proof.
"folklore":
According to János Pach, this probabilistic proof has been independently rediscovered several times, by Lovász, Matousek, Füredi, Alon, Seidel, and many others, but was not published since it is essentially equivalent to the original counting argument of Ajtai et al. The proof was first published by Székely. Using a more complicated probabilistic argument, Pach and Tóth (Proc. Graph Drawing '96, Springer LNCS 1190, 1997, pp. 345-354) recently improved the constant from 1/64 to 4/135, which is currently the best known.
 Halving lines and k-sets -
Open Problems -
Jeff Erickson
(jeffe@cs.duke.edu)
24 Feb 1998
Halving lines and k-sets -
Open Problems -
Jeff Erickson
(jeffe@cs.duke.edu)
24 Feb 1998