Abstract:
We present two new algorithms for finding the minimum-measure simplex determined by a set of n points in Rd, for arbitrary d\ge 2. The first algorithm runs in time O(nd log n) using O(n) space. The only data structure used by this algorithm is a stack. The second algorithm runs in time O(nd) using O(n2) space, which matches the best known time bounds for this problem in all dimensions and exceeds the previous best space bounds for all d>3. We also present a new optimal algorithm for building one-dimensional multiplicatively weighted Voronoi diagrams that runs in linear time if the points are already sorted.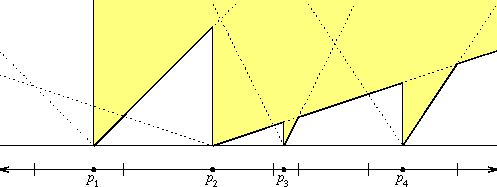
Publications -
Jeff Erickson
(jeffe@cs.uiuc.edu)
15 Nov 1999
We present two new algorithms for finding the minimum-measure simplex determined by a set of n points in Rd, for arbitrary d\ge 2. The first algorithm runs in time O(nd log n) using O(n) space. The only data structure used by this algorithm is a stack. The second algorithm runs in time O(nd) using O(n2) space, which matches the best known time bounds for this problem in all dimensions and exceeds the previous best space bounds for all d>3. We also present a new optimal algorithm for building one-dimensional multiplicatively weighted Voronoi diagrams that runs in linear time if the points are already sorted.
Publications -
Jeff Erickson
(jeffe@cs.uiuc.edu)
15 Nov 1999