
The Jordan Curve Theorem and its generalizations are the formal foundations of many results, if not every result, in two-dimensional topology. In its simplest form, the theorem states that any simple closed curve partitions the plane into two connected subsets, exactly one of which is bounded. Although this statement is intuitively clear, perhaps even obvious, the generality of the term “simple closed curve” makes a formal proof of the theorem incredibly challenging. A complete proof must work not only for sane curves like circles and polygons, but also for more exotic beasts like fractals and space-filling curves. Fortunately, these exotic curves rarely occur in practice, except as counterexamples in point-set topology textbooks.
A full proof of the Jordan Curve Theorem requires machinery that we won’t cover in this class (either point-set topology or singular homology). Here I’ll consider only the important special case of simple polygons. Polygons are by far the most common type of closed curve employed in practice, so this special case has immediate practical consequences.
Most published proofs of the full Jordan Curve Theorem both dismiss this special case as trivial and rely on it as a key lemma. Indeed, the proof is ultimately elementary. Nevertheless, the Jordan Polygon Theorem and its proof are the foundation of several fundamental algorithmic tools in computational geometry and topology.
A path in the plane is an arbitrary continuous function \(\pi\colon [0, 1] \to \mathbb{R}^2\), where \([0, 1]\) is the unit interval on the real line. The points \(\pi(0)\) and \(\pi(1)\) are called the endpoints of the path. A closed curve (or cycle) in the plane is a continuous function from the unit circle \(S^1 = \{(x,y)\in\mathbb{R}^2 \mid x^2+y^2=1\}\) to the plane.
A path or cycle is simple if it is injective, or intuitively, if it does not “self-intersect”. To avoid excessive formality, we do not normally distinguish between a simple path or cycle (formally a function) and its image (formally a subset of the plane).1
A subset \(X\) of the plane is (path-)connected if there is a path in \(X\) from any point in \(X\) to any other point in \(X\). A (path-)component of \(X\) is a maximal path-connected subset of \(X\).
A polygonal chain is a path that passes through a finite sequence of points \(p_0, p_1, \dots, p_n\), such that for each index \(i\), the subpath from \(p_{i-1}\) to \(p_i\) is the straight line segment \(p_{i-1}p_i\). The points \(p_i\) are called the vertices of the polygonal chain, and the segments \(p_{i-1}p_i\) are called its edges. We usually assume without loss of generality that no pair of consecutive edges is collinear, and in particular, that no two consecutive vertices coincide.
A polygonal chain is closed if it has at least one edge and its first and last vertices coincide (that is, if \(p_0 = p_n\)) and open otherwise. Closed polygonal chains are also called polygons; a polygon with \(n\) vertices and \(n\) edges is also called an \(n\)-gon. We can regard any polygon as a closed curve in the plane. Every simple polygon has at least three vertices.

Let me emphasize that even though this theorem considers only polygonal closed curves, the definitions of “connected” and “component” allows for arbitrary paths between points.
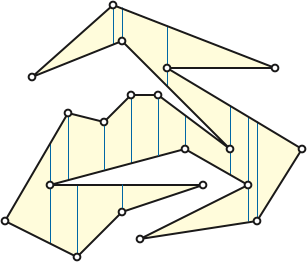
Fix a simple polygon \(P\) with \(n\) vertices. Without loss of generality, assume no two vertices of \(P\) have equal \(x\)-coordinates. The vertical lines through the vertices partition the plane into \(n+1\) slabs, two of which (the leftmost and rightmost) are actually halfplanes. The edges of \(P\) subdivide each slab into a finite number of regions we call trapezoids, even though some of these regions are actually triangles, and others are unbounded in one or more directions.
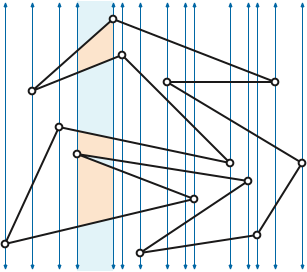
The boundary of each trapezoid consists of (at most) four line segments: the floor and ceiling, which are segments of polygon edges, and the left and right walls, which are segments of the vertical slab boundaries. The endpoints of each vertical wall (if any) lie on the polygon \(P\).
Formally, we define each trapezoid to include its walls but not its floor, its ceiling, or any vertex on its walls. Thus, each trapezoid is connected, any two trapezoids intersect in a common wall or not at all, and the union of all the trapezoids is \(\mathbb{R}^2\setminus P\). In particular, a trapezoid is a convex (and therefore connected) region in the plane, but it is not a polygon!
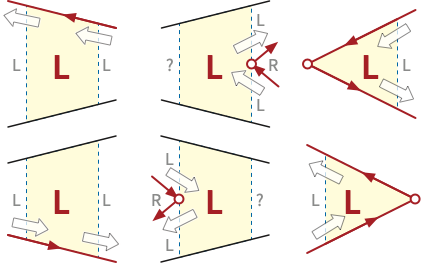
Now imagine imagine walking once around the polygon, facing directly forward along edges and turning at vertices, and consider the sequence of trapezoids immediately to our left, as suggested by the white arrows in Figure 2 above. Without loss of generality, start at the leftmost vertex \(p_0\). Whenever we traverse a directed edge \(p_{i-1}p_i\) from right to left, our left hand sweeps through all trapezoids immediately below that edge. Whenever we reach a vertex \(p_i\) whose neighbors are both to the right of \(p_i\), where the edges make a right (clockwise turn), our hand sweeps through the trapezoid just to the left of \(p_i\). The other cases are symmetric. The resulting sequence of trapezoids contains every left trapezoid at least once (and at most four times); moreover, any adjacent pair of trapezoids in this sequence share a wall and thus have a connected union. So the union of the left trapezoids is connected.
A symmetric argument implies that the union of the right trapezoids is also connected, which completes the proof.
It’s worth noting here that Lemma \(\le\) 2 holds for simple closed curves on arbitrary surfaces, including non-orientable surfaces like the Klein bottle, but it can fail for more complex topological spaces.
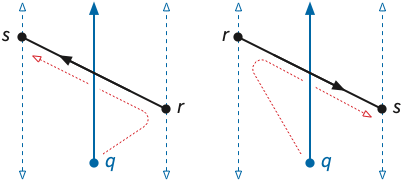
Consider any path \(\pi\) that intersects exactly two trapezoids \(\tau\) and \(\tau’\). If \(\tau\) and \(\tau’\) lie in the same slab, this path must intersect at least one edge of \(P\). (I am not invoking the Jordan curve theorem here, but rather a much more basic fact called the plane separation axiom.2) Otherwise, \(\tau\) and \(\tau’\) must lie in adjacent slabs, because \(\pi\) is continuous, and therefore must share a vertical wall.
Suppose this wall lies on the vertical line \(\ell\) through \(p_i\), and without loss of generality, \(\tau\) lies on the left of \(\ell\) and \(\tau’\) on the right. If vertices \(p_{i-1}\) and \(p_{i+1}\) are on opposite sides of \(\ell\), exactly the same number of polygon edges are above \(\tau\) and above \(\tau’\). Suppose \(p_{i-1}\) and \(p_{i+1}\) lie to the left of \(\ell\). If \(p_i\) lies below the wall \(\tau\cap\tau’\), then \(\tau\) and \(\tau’\) are below the same number of edges; otherwise, \(\tau\) is below two more edges than \(\tau’\). Similar cases arise when \(p_{i-1}\) and \(p_{i+1}\) both lie to the right of \(\ell\). In all cases, \(\tau\) and \(\tau’\) have the same parity.
More generally, consider any two trapezoids \(\tau\) and \(\tau’\) in the same component of \(\mathbb{R}^2\setminus P\). There must be a path \(\pi\colon [0,1]\to \mathbb{R}^2\setminus P\) with \(\pi(0)\in \tau\) and \(\pi(1)\in \tau’\). Let \(\tau_0, \tau_1, \dots, \tau_N\) be the sequence of trapezoids that \(\pi\) intersects, sorted in order of their first intersection. Thus, \(\tau_0 = \tau\) and for each index \(i>0\), the path \(\pi\) enters trapezoid \(\tau_i\) for the first time from some trapezoid \(\tau_j\) with \(j<i\). Our earlier arguments imply that \(\pi\) must leave \(\tau_j\) and enter \(\tau_i\) through a common wall, so these two trapezoids have the same parity. It follows by induction that every trapezoid \(\tau_i\) has the same parity as \(\tau_0\); in particular, \(\tau\) and \(\tau’\) have the same parity.
We conclude that any two trapezoids in the same component of \(\mathbb{R}^2\setminus P\) have the same parity, which completes the proof.
It’s worth noting here that Lemma \(\le\) 2 holds for more complex planar shapes, such as polygons with holes, but it fails for any surface that is no homeomorphic to a subspace of the sphere.
The Jordan Polygon Theorem now follows immediately from Lemmas \(\le 2\) and \(\ge 2\). In particular, if the polygon is oriented counterclockwise (the way god intended), then “right” and “even” (and blue) mean “outside”, and “left” and “odd” (and orange) mean “inside”.
In contexts where polygons are assumed to be simple, it is standard practice to use the single word ”polygon” (and the same variable names, and the same data structures) to refer both to a simple closed polygonal chain and to (the closure of) the interior of that polygonal chain, with the precise meaning hopefully clear from context. For example, the slab decomposition we used in this section decomposes the polygon into trapezoids, and in later lectures we will consider polygons with holes. This polysemy is justified by the Jordan Polygon Theorem.
The parity proof of Lemma \(\ge 2\) immediately suggests a standard algorithm to test whether a point lies in the interior of a simple polygon in the plane in linear time: Shoot an arbitrary ray from the query point, count the number of times this ray crosses the polygon, and return \(\textsf{true}\) if and only if this number is odd. This algorithm appears in Gauss’ notes (written around 1830 but only published after his death); it has been rediscovered many times since then.
To make the ray-parity algorithm concrete, we need one numerical primitive from computational geometry. A triple \((q, r, s)\) of points in the plane is oriented counterclockwise if walking from \(q\) to \(r\) and then to \(s\) requires a left turn, or oriented clockwise if the walk requires a right turn. More explicitly, consider the \(3\times 3\) determinant \[ \Delta(q,r,s) = \det \begin{bmatrix} 1 & q.x & q.y \\ 1 & r.x & r.y \\ 1 & s.x & s.y \end{bmatrix} = (r.x - q.x)(s.y - q.y) - (r.y - q.y)(s.x - q.x). \] The triple \((q,r,s)\) is oriented counterclockwise if \(\Delta(q,r,s) > 0\), oriented clockwise if \(\Delta(q,r,s) < 0\), and collinear if \(\Delta(q,r,s) = 0\). (The absolute value of \(\Delta(q,r,s)\) is twice the area of the triangle \(\triangle qrs\).)
Straightforward case analysis implies that the vertical ray from \(q\) crosses the line segment \(rs\) if and only if \(q\) lies between the vertical lines through \(r\) and \(s\), and \(\Delta(q,r,s)\) has the same sign as \(r.x-s.x\).
Finally, here is the algorithm in (pseudo)Python. The input polygon \(P\) is represented by an array of consecutive vertices. The algorithm returns \(+1\), \(-1\), or \(0\) to indicate that the query point \(q\) lies inside, outside, or directly on \(P\), respectively. To correctly handle ties between \(x\)-coordinates, the algorithm treats any polygon vertex on the vertical line through \(q\) (but not actually coincident with \(q\)) as though it were slightly to the left. The algorithm clearly runs in \(O(n)\) time.
def PtInPolygon(P, q):
sign = -1 // outside if no crossings
n = len(P)
for i in range(n):
r = P[i]
s = P[(i+1)% n]
Delta = (r.x - q.x)*(s.y - q.y) - (r.y - q.y)*(s.x - q.x)
if s.x <= q.x < r.x // positive crossing?
if Delta > 0:
sign = -sign
elif Delta == 0:
return 0
elif r.x <= q.x < s.x // negative crossing?
if Delta < 0:
sign = -sign
elif Delta == 0:
return 0
return signMost algorithms that operate on simple polygons actually require a decomposition of the polygon into simple pieces that are easier to manage. We’ve already seen one such decomposition, first into vertical slabs, and then into trapezoids. For many geometric and topological algorithms, the most natural decomposition breaks the interior of the polygon into triangles that meet edge-to-edge. More formally, a triangulation is a triple of sets \((V, E, T)\) with the following properties.
The third condition guarantees that the intersection of any two triangles in \(T\) is either an edge of both, a vertex of both, or empty.
If the union of the triangles in \(T\) is equal to the closure of the interior of a simple polygon \(P\), we call \((V, E, T)\) a triangulation of \(P\). If moreover \(V\) is the set of vertices of \(P\), then \((V, E, T)\) is called a frugal triangulation of \(P\). Every edge of a frugal triangulation is either an edge of \(P\) or an (interior) diagonal, meaning a line segment between two vertices of \(P\) whose interior lies in the interior of \(P\).
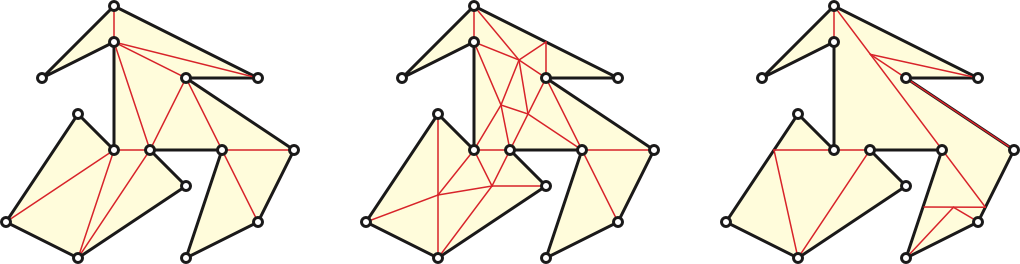
After playing with a few examples, it may seem obvious that every simple polygon has a frugal triangulation, but a formal proof of this fact is surprisingly subtle; several incorrect (or at least incomplete) proofs appear in the literature. The first complete, correct, axiomatic proofs were developed by Dehn (1899, unpublished) and Lennes (1911), although some components of their arguments already appear in the Gauss’s posthumously published notes.
The following proof is somewhat more complicated (and intentionally less formal!) than Dehn’s and Lennes’s arguments, but it directly motivates a faster algorithm for constructing triangulations.
Every trapezoid in the decomposition has exactly two polygon vertices on its boundary. Call a trapezoid boring if the line segment between these two vertices cuts through the interior of the trapezoid, and therefore is a diagonal of \(P\), and interesting otherwise. Every interesting trapezoid either has two vertices of \(P\) on its ceiling, or two vertices of \(P\) on its floor.
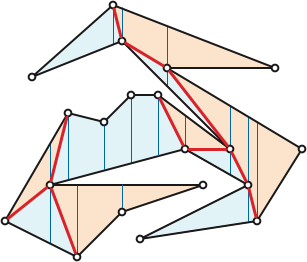
If any of the trapezoids is boring, we immediately have a diagonal. Yawn.
Any path through the interior of \(P\) that starts in a ceiling trapezoid and ends in a floor trapezoid must pass through a boring trapezoid. So if every trapezoid is interesting, then every trapezoid is interesting the same way—either every trapezoid has two vertices on its ceiling, or every trapezoid has two vertices on its floor. Thus, \(P\) is a special type of polygon we call a monotone mountain: any vertical line intersects at most two edges of \(P\), and the leftmost and rightmost vertices of \(P\) are connected by a single edge of \(P\).
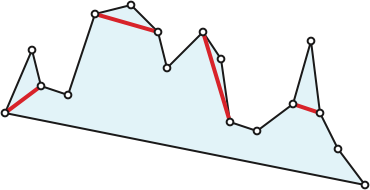
Without loss of generality, suppose \(p_0\) is the leftmost vertex, \(p_{n-1}\) is the rightmost vertex, and every other vertex is above the edge \(p_0p_{n-1}\) (so every trapezoid has two vertices on its ceiling). Call a vertex \(p_i\) convex if the interior angle at that vertex is less than \(\pi\), or equivalently, if the triple \((p_{i-1}, p_i, p_{i+1})\) is oriented clockwise. Every monotone mountain has at least one convex vertex \(p_i\) other than \(p_0\) and \(p_{n-1}\); take, for example, the vertex furthest above the floor \(p_0p_{n-1}\). For any such vertex \(p_i\), the line segment \(p_{i-1}p_{i+1}\) is a diagonal.
Let \(P\) be a simple polygon with \(n\) vertices \(p_0, p_1, p_2, \dots, p_{n-1}\). If \(P\) is a triangle, it has a trivial triangulation, so assume \(n>3\). Suppose without loss of generality (reindexing the vertices if necessary) that \(d = p_0p_i\) is a diagonal of \(P\), for some index \(i\). Let \(P^+\) and \(P^-\) denote the polygons with vertices \(p_0, p_i, p_{i+1}, \dots, p_{n-1}\) and \(p_0, p_1, p_2, \dots, p_i\), respectively. The definition of “diagonal” implies that both \(P^+\) and \(P^-\) are simple. Color each edge of \(P\) red if it is an edge of \(P^+\) and blue otherwise; every blue edge is an edge of \(P^-\).
Now we need to prove that the diagonal \(d\) partitions the interior of \(P\) into the interiors of \(P^+\) and \(P^-\). Proving this claim is surprisingly subtle.
Let \(U\) be any open disk in the interior of \(P\) that intersects \(d\); such a disk exists because \(d\) is an interior diagonal. (We had to use that fact somewhere!) The set \(U\setminus p_0p_i\) has exactly two components.[^pasch2] Choose arbitrary points \(q^+\) and \(q^-\), one in each component. Let \(R^+\) and \(R^-\) be parallel rays starting at \(q^+\) and \(q^-\), respectively, such that \(R^+\) contains \(R^-\). Then \(R^+\) crosses \(d\) but \(R^-\) does not, and \(R^+\) and \(R^-\) cross exactly the same edges of \(P\).
[^pasch2] We are invoking the plane separation axion again here.
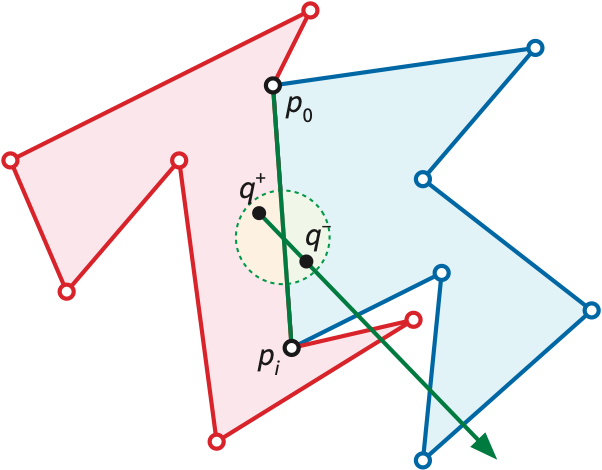
As above, \(R^+\) (and therefore \(R^-\)) crosses an odd number of edges of \(P\). Without loss of generality, suppose \(R^+\) (and therefore \(R^-\)) crosses an even number of red edges and an odd number of blue edges. Then, because \(R^+\) crosses \(d\), the point \(q^+\) lies inside \(P^+\) and outside \(P^-\). Similarly, \(q^-\) lies inside \(P^-\) and outside \(P^+\), because \(R^-\) does not cross \(d\). We conclude (finally!) that the interiors of \(P^+\) and \(P^-\) are disjoint subsets of the interior of \(P\). Whew!
The inductive hypothesis implies that \(P^+\) has a frugal triangulation \((V^+, E^+, T^+)\) and that \(P^-\) has a frugal triangulation \((V^-,E^-,T^-)\). One can now verify mechanically that \((V^+\cup V^-,\) \(E^+\cup E^-, T^+\cup T^-)\) is a frugal triangulation of \(P\).
The proof of the diagonal lemma implies an efficient algorithm to triangulate any simple polygon. I’ll only sketch the algorithm here; for further details, see your favorite computational geometry textbook. First, we construct a trapezoidal decomposition in \(O(n\log n)\) time using a sweepline algorithm. Intuitively, we sweep a vertical line from left to right across the plane, maintaining its intersection with the polygon in a balanced binary search tree, and inserting a new vertical wall whenever the line touches a vertex. (In fact, we only visit the vertices in order from left to right.) Second, we insert diagonals inside every boring trapezoid; these diagonals decompose \(P\) into monotone mountains in \(O(n)\) time. Finally, we triangulate each monotone mountain in \(O(n)\) time by cutting off convex vertices in order from left to right.
The overall running time is \(O(n\log n)\); the running time is dominated by the time to construct the trapezoidal decomposition. Theoretically faster algorithms for that construction are known—in particular, Chazelle described a famously complex \(O(n)\)-time algorithm—but it is unclear whether any of these improvements is faster in practice, or indeed if any of them have actually been implemented.
I’ll leave the following corollaries of the polygon triangulation theorem as exercises.
Mark de Berg, Otfried Cheong, Marc van Kreveld, and Mark Overmars. Computational Geometry: Algorithms and Applications, 3rd edition. Springer-Verlag, 2008. Your favorite computational geometry textbook.
Bernard Bolzano. Anti-Euklid. Unpublished manuscript, c. 1840. Published posthumously in [10].
Max Dehn. Beweis des Satzes, daß jedes geradlinige geschlossene Polygon ohne Doppelpunkte ‘die Ebene in zwei Teile teilt’. Unpublished manuscript, c.1899. Max Dehn Papers archive, University of Texas at Austin. Cited and described in detail by Guggenheimer [4]. Proof of the Jordan Polygon Theorem.
Heinrich W. Guggenheimer. The Jordan curve theorem and an unpublished manuscript of Max Dehn. Arch. History Exact Sci. 17:193–200, 1977.
Camille Jordan. Courbes continues. Cours d’Analyse de l’École Polytechnique, 1st edition, vol. 3, 587–594, 1887.
Camille Jordan. Lignes continues. Cours d’Analyse de l’École Polytechnique, 2nd edition, vol. 1, 90–99, 1893.
Nels Johann Lennes. Theorems on the simple finite polygon and polyhedron. Amer. J. Math. 33:37–62, 1911. Read to the AMS in April, 1903. Proof of the Jordan Polygon Theorem.
Joseph O’Rourke. Computational Geometry in C, 2nd edition. Cambridge University Press, 1998. Your favorite computational geometry textbook.
Moritz Pasch. Vorlesung über neuere Geometrie. Teubner, 1882.
Kazimír Večerka. Bernard Bolzano: Anti-Euklid. Sbornik pro dějiny přirodnich věd a teckniky / Acta Hist. Rerum Natur. Nec Non Tech. 11:203–216, 1967. In Czech, with German summary.
Historically, the definition of “simple closed curve” was a point of serious confusion for several decades, starting with Bolzano around 1840s. This confusion was finally resolved only when Jordan defined closed curves as functions instead of subsets of the plane.↩︎
The plane separation axiom states that the complement \(\mathbb{R}^2\setminus \ell\) of any straight line \(\ell\) in the plane has exactly two components. This axiom follows easily from the intermediate value theorem; it is also formally equivalent to Pasch’s axiom: If a line \(\ell\) does not contain any vertex of a triangle \(\triangle\), then \(\ell\) intersects an even number of edges of \(\triangle\). In 1882, Moritz Pasch proved that his axiom is independent of Euclid’s postulates, but that some theorems in the Elements require it. Yes, there is such a thing as non-Paschian geometry. It’s weeeeeird.↩︎