So far we have not assumed that planar embeddings are in any way well-behaved geometrically; edges can be embedded as arbitrarily pathological paths. It is not hard to prove using a compactness argument (Similar to the simplicial approximation theorem for homotopy) that every planar graph has a piecewise-linear planar embedding, where every edge is embedded as a simple polygonal path.
But in fact, every simple planar graph has a straight-line embedding, where every edge is represented by a single straight line segment. More strongly, any planar embedding is equivalent to (meaning it has the same rotation system as) a straight-line embedding. This result was first proved (indirectly) by Steinitz (1916), and then independently rediscovered by Wagner (1936), [Cairns (1944)], Fáry (1948), Stein (1951), Stojaković (1959), and Tutte (1960), so of course it’s usually called “Fáry’s theorem”.
Non-simple planar graphs do not have straight-line embeddings; in any such embedding, parallel edges would coincide and loops would degenerate to points. But every planar map can be transformed into a simple map by subdividing loops into cycles of length \(3\) and parallel edges into paths of length \(2\). It (finally!) follows that any generic planar curve with \(n\) vertices is equivalent to a planar polygon with at most \(3n\) vertices.
The existence of straight-line maps for simple planar graphs finally gives us the converse of Euler’s theorem:.
Moreover, all of the proofs described in this note are constructive; in particular, they all imply linear-time algorithms to construct straight-line embeddings from a given planar rotation system.
Throughout this note, we’ll consider the special case of simple triangulations: simple planar maps in which every face is bounded by three edges.
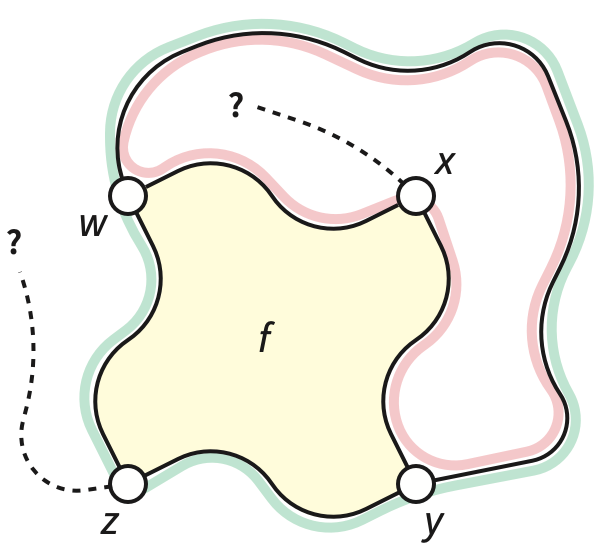
For ease of presentation, assume \(f\) is bounded. Suppose \(\Sigma\) contains an edge between \(w\) and \(y\), necessarily outside \(f\). The vertices \(w\) and \(y\) subdivide the boundary of \(f\) into two paths, one through \(x\) and the other through \(z\). Adding the edge \(wy\) to those paths creates two cycles. Without loss of generality, \(x\) lies in the interior of the cycle \(C\) that passes through \(z\); as shown in Figure 1.
Now suppose for the sake of argument that \(\Sigma\) also contains an edge \(xz\), again necessarily outside \(f\). This edge passes through the exterior of \(C\) near \(z\), but it also passes through the interior of \(C\) near \(x\). So the Jordan Curve Theorem implies that \(xz\) intersects \(C\), contradicting the definition of embedding. \(\qquad\square\)

To compute a straight-line map \(\overline\Sigma\) equivalent to an arbitrary simple planar map \(\Sigma\), it suffices to add edges to \(\Sigma\) to obtain a simple planar triangulation \(T\), compute a straight-line map \(\overline{T}\) equivalent to \(T\), and then delete the (straightened) added edges.
In the following sections, I’ll describe three different constructions of straight-line triangulations equivalent to a given triangulation \(T\).
A simple polygon \(P\) is star-shaped if there is at least one interior point \(q\) such that for each vertex \(p\) of \(P\), the segment \(pq\) does not cross any edge of \(P\). The set of all such points \(q\) is called the kernel of \(P\).
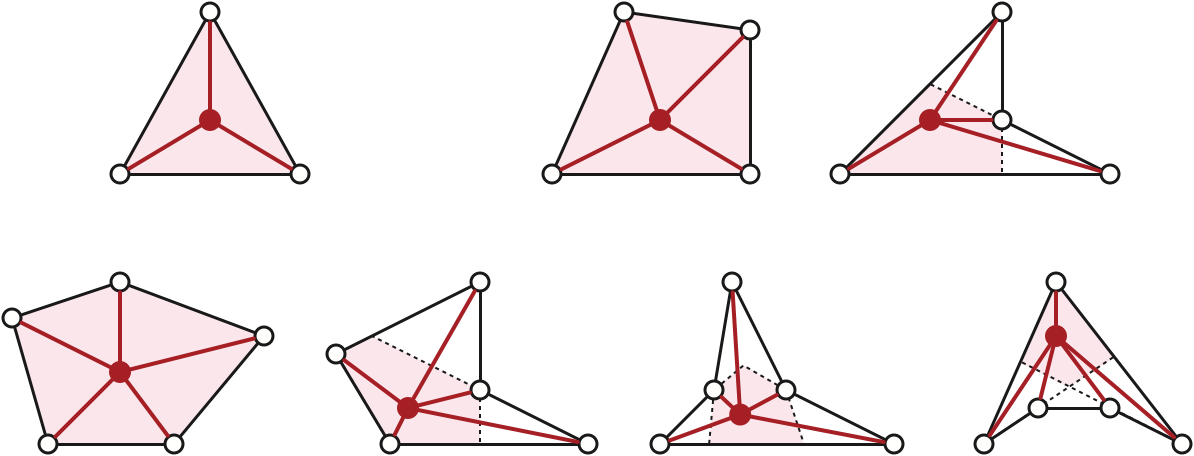
Let \(v\) be any interior vertex of \(T\) with degree at most \(5\). Deleting \(v\) creates a face \(f\) with degree \(\deg(v)\). We extend \(T\setminus v\) to a simple triangulation \(T’\) by adding \(\deg(v)-3\) diagonals inside \(f\), following the Triangulation Lemma. The induction hypothesis implies that \(T’\) is equivalent to a straight-line triangulation \(\overline{T}’\). Deleting the diagonals yields a simple planar map \(\overline{T\setminus v}\) equivalent to \(T\setminus v\). The face \(\overline{f}\) of \(\overline{T\setminus v}\) corresponding to \(f\) is a simple polygon with \(\deg(v)\le 5\) vertices. Inserting a vertex \(\overline{v}\) in the kernel of \(\overline{f}\) and connecting \(\overline{v}\) to every vertex of \(\overline{f}\) yields a straight-line triangulation \(\overline{T}\) equivalent to \(T\). \(\qquad\square\)
Here is a second inductive proof of the Straight-Line Triangulation Theorem that does not rely on Euler’s formula, roughly following an argument of de Fraysseix, Pach, and Pollack (1988). This proof is close in spirit to early flawed inductive proofs of Euler’s formula, including Euler’s own flawed proof.
We actually prove the following stronger claim: Let \(\Sigma\) be any simple planar map whose interior faces are triangles and whose outer face is bounded by a simple cycle of length \(h\ge 3\). Let \(v_1, v_2, \dots, v_h\) be the vertices of the outer face of \(\Sigma\) in counterclockwise order. Let \(P\) be any convex polygon with vertices \(p_1, p_2, \dots, p_h\) in counterclockwise order. Then there is a straight-line planar map \(\overline{\Sigma}\) that is equivalent to \(\Sigma\), whose outer face is \(P\), such that each outer vertex \(v_i\) corresponds to the polygon vertex \(p_i\).
The proof proceeds by induction on the number of vertices of \(\Sigma\). If \(\Sigma\) is a single triangle, the claim is trivial, so assume otherwise. There are two nontrivial cases to consider: Either \(v_1\) and \(v_{h-1}\) are the only neighbors of \(v_h\) on the outer face, or \(v_h\) has another neighbor \(v_j\) on the outer face.
In this case, we recursively compute a straight-line planar map equivalent to \(\Sigma\setminus v_h\) and then embed the edges incident to \(v_h\) as line segments.
Specifically, let \(w_1, w_2, \dots, w_d\) be the neighbors of \(v_h\), indexed in order around \(v_h\) so that \(w_1 = v_{h-1}\) and \(w_d = v_1\). The vertices \(w_2, \dots, w_{d-1}\) all lie in the complement of the outer face, and \(\Sigma\) contains the edge \(w_i w_{i+1}\) for every index \(i\). It follows that the outer face of the submap \(\Sigma’ = \Sigma\setminus v_h\) is bounded by a simple cycle with vertices \(v_1, v_2, \dots, v_{h-1}=w_1, w_2, \dots, w_d=v_1\). Every bounded face of \(\Sigma’\) is also a bounded face of \(\Sigma\) and thus has degree \(3\).
Now let \(\alpha\) be a convex arc from \(p_1\) to \(p_{h-1}\) inside the triangle \(p_1 p_h p_{h-1}\). (For example, \(\alpha\) could be a circular arc tangent to \(p_1 p_h\) at \(p_1\) and tangent to \(p_h p_{h-1}\) at \(p_{h-1}\).) Place \(d\) evenly spaced points \(q_1, q_2, q_3, \dots, q_d\) along \(\alpha\), with \(q_1 = p_{h-1}\) and \(q_d = p_1\). Finally, let \(P'\) be the convex polygon obtained by replacing the edges \(p_{h-1}p_h\) and \(p_hp_1\) with the polygonal chain \(q_1 q_2 \dots q_d\).
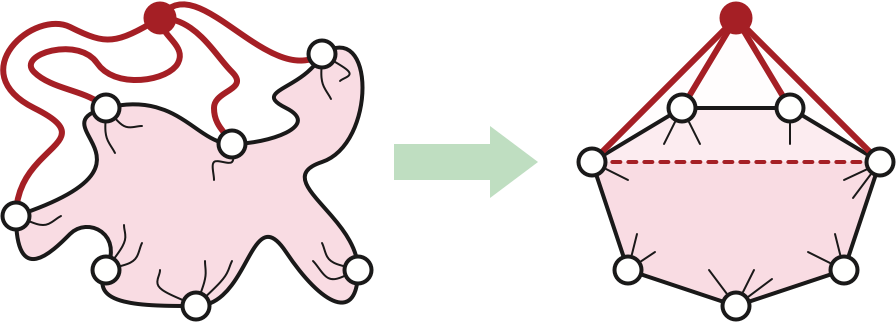
The inductive hypothesis implies that there is a straight-line embedding \(\overline{\Sigma’}\) equivalent to \(\Sigma’\) with outer face \(P'\), that maps each vertex \(v_i\) (with \(i\ne h\)) to the corresponding point \(p_i\) and each vertex \(w_i\) to the corresponding point \(q_i\). Adding the edges \(p_h q_i\) gives us a straight-line map \(\overline{\Sigma}\) equivalent to \(\Sigma\) with outer face \(P\) and the required vertex correspondences.
Now suppose \(v_h\) is adjacent to some vertex \(v_j\) on the outer face besides \(v_1\) and \(v_{h-1}\). In this case, we split \(\Sigma\) into two submaps along the edge \(v_h v_j\), split the polygon \(P\) into two smaller polygons along the diagonal \(p_hp_j\), and recursively embed each fragment of \(\Sigma\) into the corresponding fragment of \(P\).
Specifically, let \(\Sigma^\sharp\) be the submap of \(\Sigma\) obtained by deleting every vertex outside the simple cycle \((v_h, v_1, v_2, \dots, v_j, v_h)\). (The outside of this cycle is well-defined by the Jordan Curve Theorem.) Similarly, let \(\Sigma^\flat\) be the submap of \(\Sigma\) obtained by deleting every vertex outside the simple cycle \((v_h, v_j, v_{j-1}, \dots, v_{h-1}, v_h)\). Both \(\Sigma^\flat\) and \(\Sigma^\sharp\) satisfy the conditions of our claim.
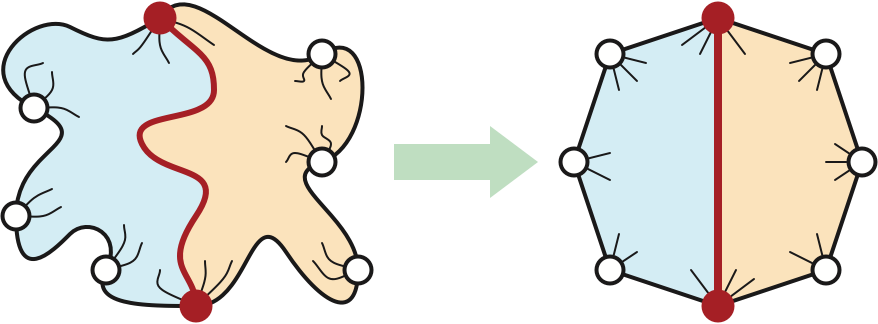
The line segment \(p_hp_j\) partitions the polygon \(P\) into two smaller convex polygons \(P^\flat\) and \(P^\sharp\). The induction hypothesis give us straight-line embeddings \(\overline{\Sigma^\flat}\) and \(\overline{\Sigma^\sharp}\), respectively equivalent to \(\Sigma^\flat\) and \(\Sigma^\sharp\), with respective outer faces bounded by \(P^\flat\) and \(P^\sharp\), mapping each vertex \(v_i\) to the corresponding point \(p_i\). In particular, in both straight-line embeddings, the the line segment \(p_hp_j\) corresponds to the edge \(v_hv_j\). Combining the straight-line embeddings \(\overline{\Sigma^\flat}\) and \(\overline{\Sigma^\sharp}\) along \(p_hp_j\) gives us the required straight-line embedding \(\overline{\Sigma}\).
The second case is actually redundant. A simple recursive argument, similar to the proof that every polygon triangulation has two ears, implies that there are at least two non-adjacent vertices on the outer face with exactly two neighbors on the outer face. It follows that the vertices of \(\Sigma\) can be ordered \(v_1, v_2, \dots, v_n\), so that after deleting any prefix \(v_1, v_2, \dots, v_i\) where \(i\le n-3\), the outer face of the remaining subgraph is bounded by a simple cycle, and the next vertex \(v_{i+1}\) lies on the outer face. This sequence of vertices is called a canonical ordering (or a vertex-shelling order) for \(\Sigma\)
In 1989, Walter Schnyder discovered a significant refinement of the previous proof, which implies that any \(n\)-vertex planar graph has a straight-line embedding whose vertices lie on an \((n-1)\times (n-1)\) integer grid. Again, we consider only simple planar triangulations, where all faces have degree \(3\), including the outer face.
Let \(T\) be a simple planar triangulation with \(n\) vertices. Schnyder defined two different ways to annotate features of \(T\) with the colors red, green, and blue. The first of these is a Schnyder coloring, which colors the interior corners subject to two conditions:
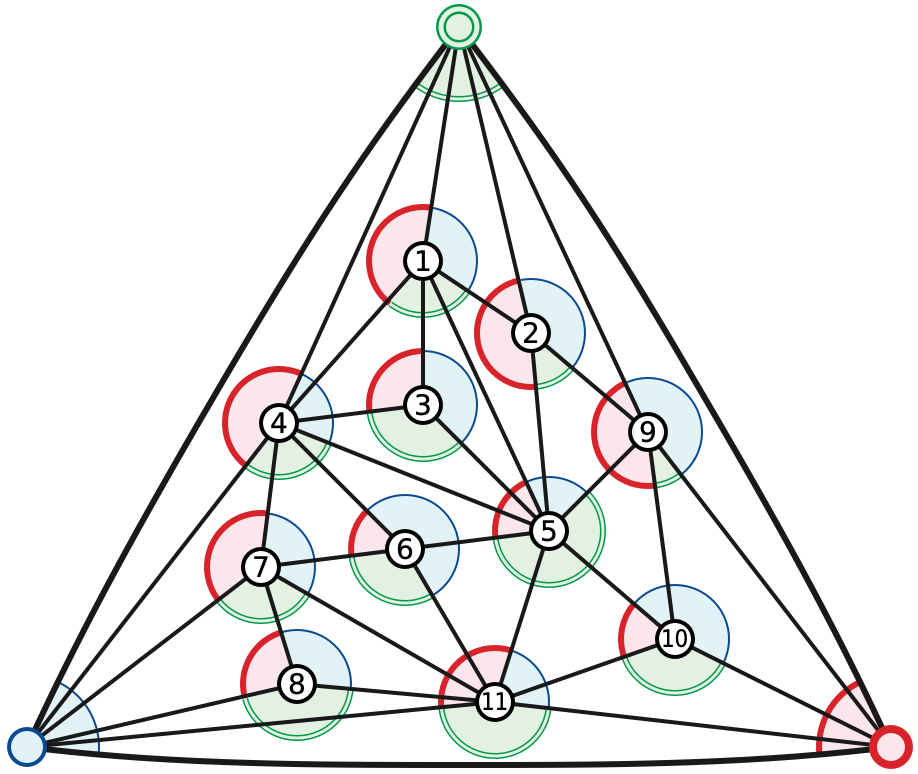
A Schnyder coloring can be constructed in linear time as follows. Color the outer vertices of \(T\) red, green, and blue in counterclockwise order. If \(T\) has a single bounded face, its three corners inherit the colors of the incident vertices. Otherwise, choose an arbitrary edge from a boundary vertex \(u\) to an interior vertex \(v\). There are two cases to consider.
Suppose \(v\) has exactly two common neighbors with \(u\). The contraction \(T/uv\) has two pairs of parallel edges; deleting one edge in each pair yields a smaller triangulation \(T’\). Recursively compute a Schnyder coloring for \(T’\), and transfer the corner colors back to \(T\). Finally, there is only one way to consistently color the faces of \(T\) on either side of \(uv\); specifically, the corners incident to the boundary vertex \(u\) inherit \(u\)’s color.
If \(v\) has at least three common neighbors with \(u\), there must be a triangle \(uvw\) in \(T\) containing at least one vertex in its interior. In this case, we recursively compute Schnyder colorings of the subgraphs of \(G\) inside \(uvw\) and outside \(uvw\). In both recursive subproblems the boundary vertex \(u\) retains its originally assigned color, so that the resulting Schnyder colorings are compatible.
In fact, the second case is unnecessary. By expanding the recursion from the second case, we see that the entire construction is carried out by a sequence of contractions; equivalently, an easy induction argument implies that at least one edge from each boundary vertex can be contracted immediately. The Schnyder coloring in the figure above was computed by contacting the interior vertices toward the top (green) vertex in the order indicated by the vertex labels.
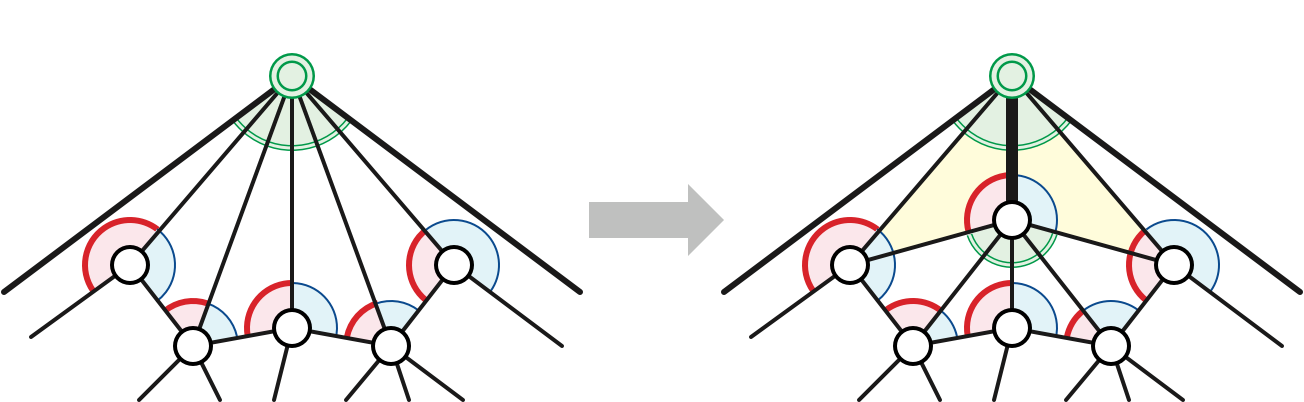
The second annotation, called a Schnyder wood, assigns a direction and a color to every internal edge of \(T\). Every internal edge in \(T\) is incident to corners with all three colors, with one color appearing twice at one endpoint. Schnyder orients each internal edge \(e\) toward the endpoint with the same color twice, and assigns the repeated color to the edge. The resulting coloring and orientation has the following useful properties:
We can also construct Schnyder woods directly using a sequence of edge contractions, just as we constructed Schnyder colorings. Expanding an edge introduces one vertex and three edges; we orient the new edges away from the new vertex, and assign them the only colors consistent with the properties listed above. Conversely, every Schnyder wood can be constructed using this algorithm, contracting toward any of the outer vertices.

Given any Schnyder wood, we can define an equivalent Schnyder coloring as follows. For any interior corner, if the two edges are both leaving the corner vertex, assign the third color to the corner; otherwise, assign the color of the incoming edge(s) to the corner.
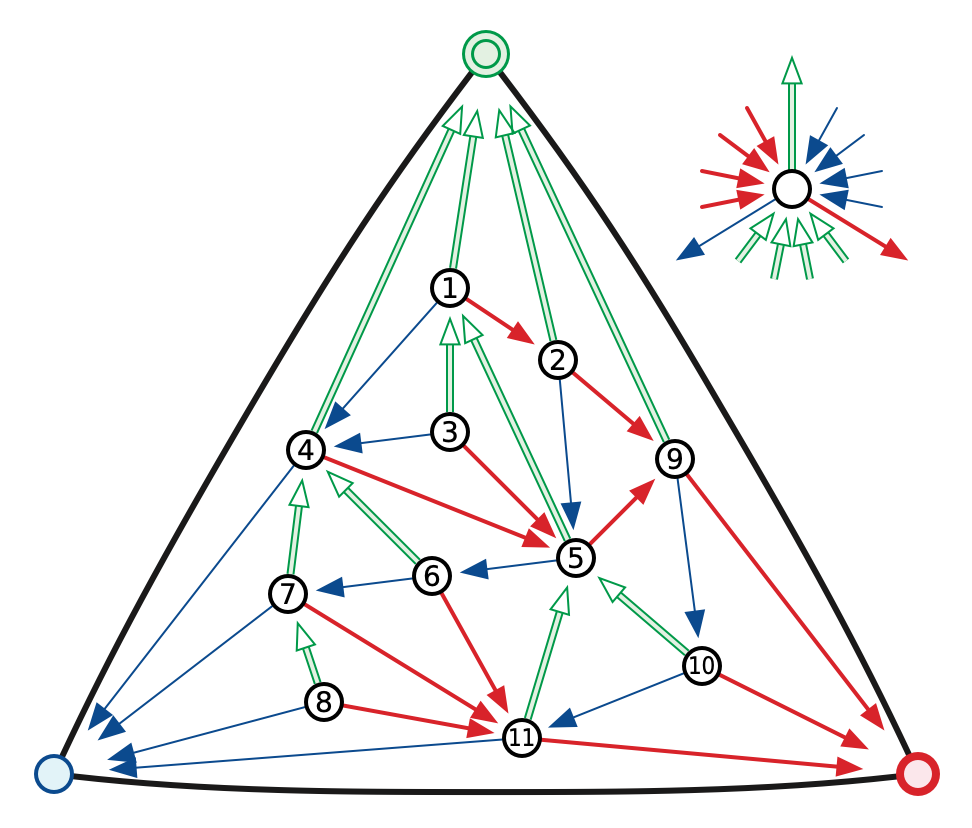
Number the interior vertices by the order in which they are contracted to the green boundary vertex, as shown in the figures. Label the green boundary vertex \(0\) and the other two boundary vertices \(\infty\). Call an edge \(v\mathord\to w\) increasing if the label of \(w\) is larger than the label of \(w\) and decreasing otherwise. Every green edge is decreasing, and every red and blue edge is increasing. Thus, none of the red, green, or blue subgraphs contains a cycle; starting from any interior node, following edges of any fixed color leads to the outer vertex of that color. \(\qquad\square\)
Hey, look, we have yet another proof of Euler’s formula!
Consider any Schnyder wood of a simple planar triangulation \(T\) with \(n\) vertices, \(m\) edges, and \(f\) faces (including the outer face). The edges of each color define a rooted tree with \(n-2\) vertices, and therefore \(n-3\) edges, and every interior edgesbelongs to exactly one such tree. It immediately follows that \(m = 3(n-3)+3 = 3n-6\). Finally, because every face is a triangle, we have \(2m = 3f = 6n-12\), so \(f = 2n-4\). We conclude that \(n-m+f = n - (3n-6) + (2n-4) = 2\). \(\qquad\square\)
Now we assign integer coordinates to every interior vertex \(v\) as follows. There is a unique path of red edges, a unique path of green edges, and a unique path of blue edges from \(v\) to the boundary. These three paths partition the triangulation into three regions, which we color red, green, and blue as shown below. Each region contains its clockwise bounding path—for example, the green region includes the blue path, including the blue boundary vertex—but not \(v\) itself.
For purposes of defining these regions when \(v\) is a boundary vertex, we orient the boundary edges clockwise and color each edge according to its head. Thus, if \(r,g,b\) are the red, green, and blue boundary vertices, the green region of \(g\) contains every vertex except \(g\) and \(r\), the red region of \(g\) contains only \(r\), and the blue region of \(g\) is empty.
For each vertex \(v\), let \(r(v)\), \(g(v)\), \(b(v)\) respectively denote the number of vertices in the red, green, and blue regions of \(v\). By definition, we have \(r(v) + g(v) + b(v) = n-1\) for every vertex \(v\).

Finally, part (d) follows by straightforward case analysis. Up to a choice of colors, there are only two cases to consider: either the edges of \(uvw\) have distinct colors (and therefore define a directed cycle), or two of the three edges have the same color (so the edges do not define a directed cycle). \(\qquad\square\)
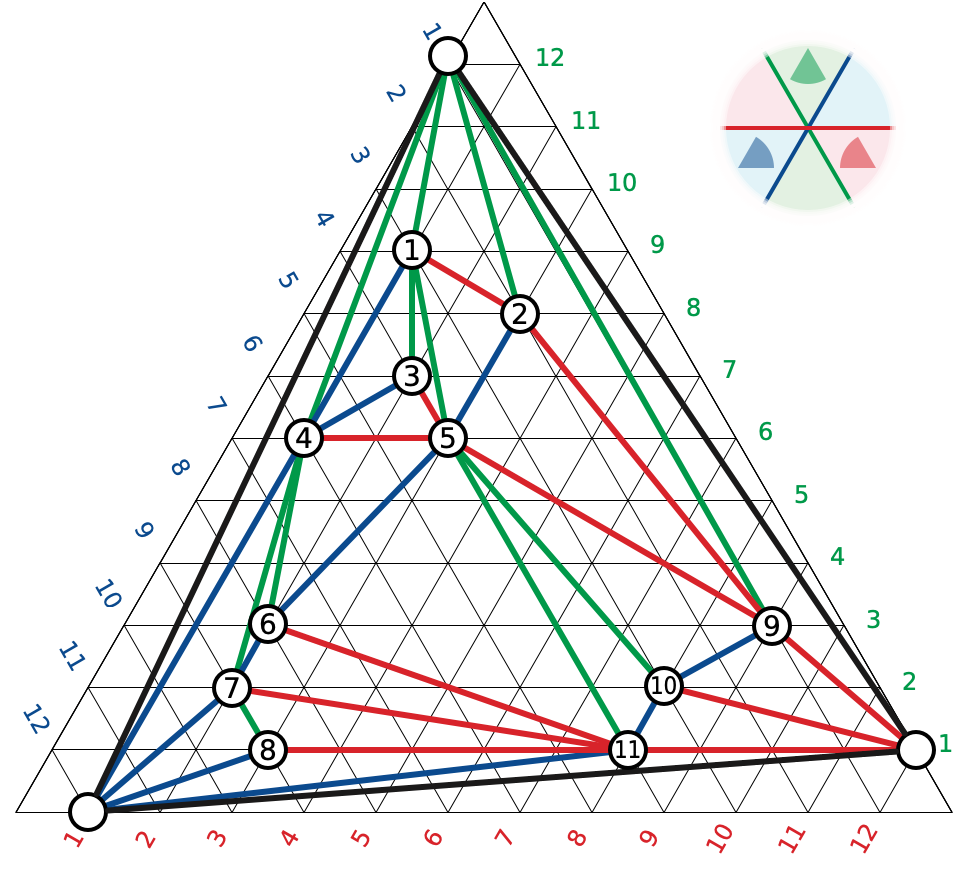
Assign each vertex \(v\) of \(T\) the integer coordinates \((g(v), b(v))\). Let \(uvw\) be an arbitrary triangle whose corners at \(u\), \(v\), and \(w\) are respectively colored red, green, and blue by the Schnyder coloring. The orientation of the new embedding of \(uvw\) is given by the sign of the determinant \[ \left|\begin{matrix} 1 & g(u) & b(u) \\ 1 & g(v) & b(v) \\ 1 & g(w) & b(w) \end{matrix}\right| ~=~ \big(g(v)-g(u)\big)\big(b(w)-b(u)\big) - \big(g(w)-g(u)\big)\big(b(v)-b(u)\big). \] The previous lemma implies that this expression is positive, which implies that the triangle is oriented counterclockwise. Because every triangle is oriented consistently, no two triangles in the embedding can overlap, and therefore no pair of edges can intersect. (The signed area of the outer triangle is equal to the sum of the signed areas of the interior triangles; if two triangles overlapped, the sum of the areas of the interior triangles would be strictly larger than the unsigned area of the outer triangle!) All vertex coordinates are integers between \(0\) and \(n-2\). \(\qquad\square\)
The following figure shows the resulting embedding for our example graph. Instead of embedding on the square grid, I’m using a grid of equilateral triangles, assigning each vertex \(v\) barycentric coordinates \((r(v), g(v), b(v))\).
Eventually….