Recall that a planar map is the decomposition of the plane (or by standard abuse of terminology, the sphere) induces by an embedding of a graph in the plane. Any planar map can be represented by a rotation system \(\Sigma = (D, \textsf{rev}, \textsf{succ})\) where \(D\) is the set of darts of the embedded graph, \(\textsf{rev}\) is the reversal involution for those darts, and \(\textsf{succ}\) is a permutation of the darts whose orbits describe the darts into each vertex of the embedded graph in clockwise order. The orbits of the permutation \(\textsf{rev}(\textsf{succ})\) describe the counterclockwise order of darts around the boundary of each face. A rotation system with \(n\) vertices, \(m\) edges, and \(f\) faces is planar if and only if \(n-m+f = 2\).
But what if \(n-m+f \ne 2\)? In that case, \(\Sigma\) represents a map on a more complex surface.
A surface (or 2-manifold) is a (compact, second-countable, Hausdorff) topological space that is locally homeomorphic to the plane. That is, every point lies in an open subset of the space that is homeomorphic to \(\mathbb{R}^2\). (Later we will also consider surfaces with boundary, spaces where every point lies in an open neighborhood homeomorphic to either the plane or a closed halfplane.)
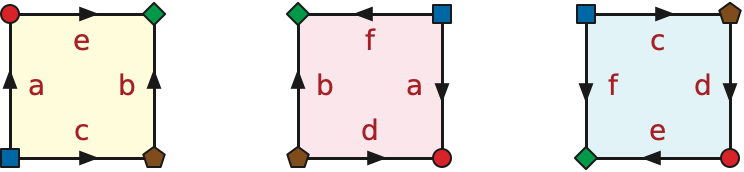
The simplest method to construct surfaces is to glue disks together along their boundary segments. A polygonal schema is a finite set of polygons with labeled edges, where each label appears exactly twice. We can construct a surface by identifying every pair of edges with the same label; specifically, if the edges of each polygon are oriented counterclockwise around its interior, we identify each edge with the reversal of the other edge with the same label. The vertices and edges of the polygons become the vertices and edges of a graph; the interiors of the polygons become the faces of the resulting embedding.
Formally, an (abstract) polygonal schema is a triple \((D, \textsf{rev}, \textsf{succ}^*)\), where \(D\) is a set of darts (representing the sides of the polygons), is an involution of those darts (representing pairs of sides with matching labels), and \(\textsf{succ}^*\) is a permutation describing the counterclockwise order of darts around each face/polygon. Hopefully it’s clear that “abstract polygonal schema” is just a synonym for “dual rotation system”.
To transform an abstract polygonal schema \(\Pi\) into a topological space, let \(F\) denote a set of disjoint closed disks in the plane, one for each orbit of \(\textsf{succ}^*\). For each orbit of length \(d\), we subdivide the counterclockwise boundary of the corresponding disk into \(d\) paths. We identify those paths with the darts, so that \(\textsf{succ}^*(d)(0) = d(1)\) for every dart/path \(d\). Then the space \(\mathcal{S}(\Pi)\) is the quotient space \(\bigsqcup F / \sim\), where \(d(t) \sim \textsf{rev}(d)(1-t)\) for every dart/path \(d\) and \(t\in[0,1]\). In other words, we identify each dart with the reversal of its reversal! It is not hard to verify that the space \(\mathcal{S}(\Pi)\) is always a 2-manifold; the vertices, edges, and faces constitute a map \(\Sigma(\Pi)\) of this surface.1
Moving in the other direction, recall that an embedding of a graph \(G = (V, \textsf{rev}, \textsf{head})\) on a surface \(\mathcal{S}\) is a continuous injective function from \(G\) (as a topological graph) into \(\mathcal{S}\). The components of the complement of the image of the embedding are the faces of the embedding. An embedding is cellular if every face is homeomorphic to an open disk. The vertices, edges, and faces of an embedding define a surface map if and only if the embedding is cellular; in particular, the embedded graph must be connected.
Any discussion of rotation systems or polygonal schemata for surface maps assumes a priori that the underlying surface is orientable, meaning it is possible to consistently define “clockwise” and “counterclockwise” everyone on the surface. As we’ll prove in the next lecture, every orientable surface can be constructed from the sphere by attaching one or more “handles”; the number of handles is called the genus of the surface. More formally, the genus of a surface \(\mathcal{S}\) is the maximum number of closed curves \(\gamma_1, \dots, \gamma_g\) in \(\mathcal{S}\) whose complement \(\mathcal{S} \setminus (\gamma_1 \cup \cdots \cup \gamma_g)\) is connected.
However, not all 2-manifolds are orientable. The simplest example of a non-orientable surface (with boundary) is the Möbius band, which can be constructed from a strip of paper by gluing opposite ends with a half-twist. More formally, the Möbius band is the quotient space \([0,1]^2 / \sim\) where \((0, t) \sim (1, 1-t)\) for all \(t\in[0,1]\). In fact, Möbius bands are the only obstruction to orientability; a surface is orientable if and only if it does not contain (a subspace homeomorphic to) a Möbius band.
In one of Lewis Carroll’s lesser-known works, one character explains to another how to sew three square handkerchiefs into “Fortunatus’s Purse” (so called because “Whatever is inside that Purse, is outside it; and whatever is outside it, is inside it. So you have all the wealth of the world in that leetle Purse!”). His instructions can be interpreted as a signed polygonal schema for a non-orientable surface map of genus 1.

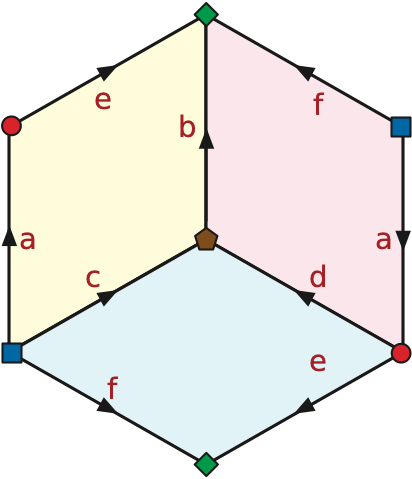
We can’t represent non-orientable surface maps using rotation systems, so we need a different combinatorial representation. It is possible to define signed versions of both rotation systems and polygonal schemata, but their navigation requires awkward bookkeeping and case analysis. Instead we consider a more elegant but slightly more verbose combinatorial representation that works for both orientable and non-orientable surfaces.
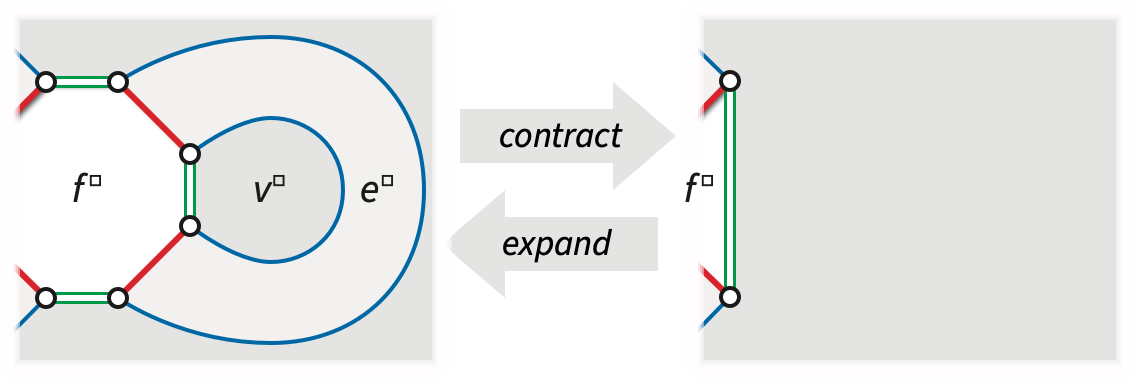
Let \(\Sigma = (V, E, F)\) be an arbitrary map of some surface \(\mathcal{S}\), which may or may not be orientable. We construct a related surface map \(\Sigma^\square\), called a band decomposition, intuitively by shrinking each face of \(\Sigma\) slightly, expanding each vertex of \(\Sigma\) into a small closed disk, and replacing each edge of \(\Sigma\) with a closed quadrilateral “band”.
If a surface map \(\Sigma\) has \(n\) vertices, \(m\) edges, and \(f\) faces, then its band decomposition \(\Sigma^\square\) has \(4m\) vertices, \(6m\) edges (\(2m\) of each type), and \(n+m+f\) faces.
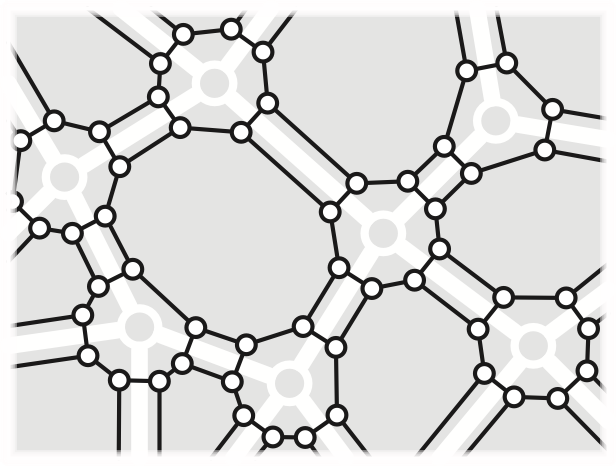
Lemma: A surface map \(\Sigma\) is orientable if and only if the graph of its band decomposition \(\Sigma^\square\) is bipartite.
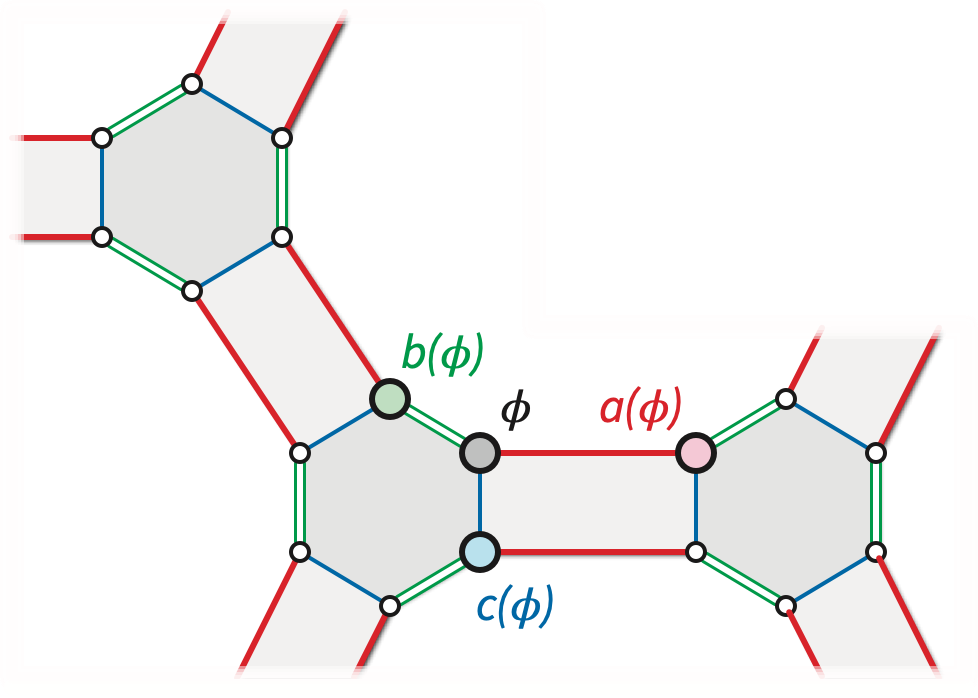
Band decompositions immediately suggest the following combinatorial representation of surface maps. A reflection system.2 is a quadruple \(\Xi = (\Phi, a, b, c)\) with the following components:
To simplify notation, I’ll use concatenation to denote compositions of the involutions \(a\), \(b\), and \(c\); thus, for example, \(ac\) is shorthand for the permutation \(a \circ c\), and \(abc(\phi)\) is shorthand for \(a(b(c(\phi)))\).
Each blade in \(\Sigma\) can be associated with a triple \((v, e, f)\), where \(e\) is an edge of \(\Sigma\), \(v\) is one of \(e\)’s endpoints, and \(f\) is one of \(e\)’s shores. Intuitively, each of the involutions \(a\), \(b\), \(c\), changes one of the components of this triple: \(a\) changes the vertex (or apex); \(b\) changes the edge (or border); \(c\) changes the face (of chamber). More formally, the orbits of the permutation group \(\langle b,c \rangle\) are the vertices of the reflection system; the orbits of \(\langle a,c \rangle\) are its edges; and the orbits of \(\langle a,b \rangle\) are its faces.
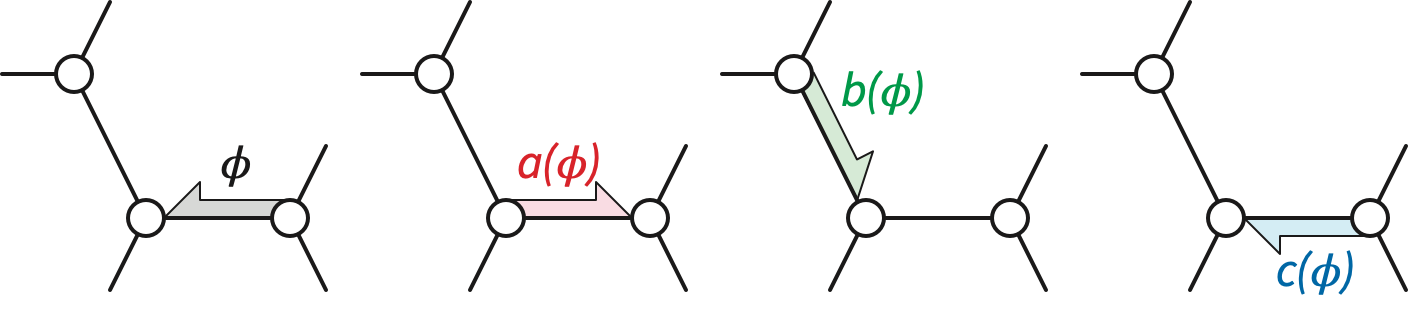
Every reflection system represents a unique surface map with corresponding blades, sides, corners, darts, vertices, edges, and faces. (In particular, the trivial reflection system with \(\Phi = \varnothing\) represents the trivial map.) Conversely, every surface map is represented by a unique reflection system.
Just as rotation systems are mathematical abstractions of incidence lists, reflection systems can also be encoded as a simple data structure for surface maps, which has one record for every blade \(\phi\), each containing the index of its head and pointers to its neighboring blades \(a(\phi)\), \(b(\phi)\), \(c(\phi)\), along with an array indexed by vertices pointing to an arbitrary blade into each vertex. (It may also be convenient to store the index of each blade’s “left” shore, and a face-indexed array pointing one blade for each face.)
A particularly simple implementation represents blades by integers from \(0\) to \(4m-1\), such that for any blade \(\phi\), the neighboring blades \(a(\phi)\) and \(c(\phi)\) are obtained by flipping the two least significant bits, for example, by defining \(a(\phi) = \phi\oplus 2\) and \(c(\phi) = \phi\oplus 1\). Thus, edge \(e\) consists of blades \(4e, 4e+1, 4e+2, 4e+3\), and blade \(\phi\) belongs to edge \(\lfloor \phi/4 \rfloor\). Then any static surface map can be represented using five arrays:
Notice that \(\textsf{vert}(\phi) = \textsf{vert}(c(\phi)) = \textsf{vert}(\phi\oplus 1)\) and \(\textsf{face}(\phi) = \textsf{face}(a(\phi)) = \textsf{face}(\phi\oplus 2)\), so in principle, exactly half of the \(\textsf{vert}\) and \(\textsf{face}\) arrays are redundant.
Transforming a rotation system of a surface map into an equivalent reflection system or vice versa (if the map is orientable) is straightforward.
Let \(\Sigma = (D, \textsf{rev}, \textsf{succ})\) be a rotation system. Then setting \(\Phi := D\times \{-1, +1\}\) and defining the involutions as follows gives us an equivalent reflection system: \[ \begin{aligned} a((d, +1)) & := (\textsf{rev}(d), -1) & a((d, -1)) & := (\textsf{rev}(d), +1) \\ b((d, +1)) & := (\textsf{succ}(d), -1) & b((d, -1)) & := (\textsf{succ}^{-1}(d), +1) \\ c((d, +1)) & := (d, -1) & c((d, -1)) & := (d, +1) \end{aligned} \]
Conversely, let \(\Xi = (\Phi, a, b, c)\) be an orientable reflection system. Because \(\Xi\) is orientable, we can partition \(\Phi\) into two subsets \(\Phi^+\) and \(\Phi^-\), so that each of the involutions \(a,b,c\) is a bijection between the two subsets. We can construct a rotation system equivalent to \(\Xi\) by setting \(D := \Phi^+\) and \(\textsf{rev} := a\circ c\) and \(\textsf{succ} := b\circ c\).
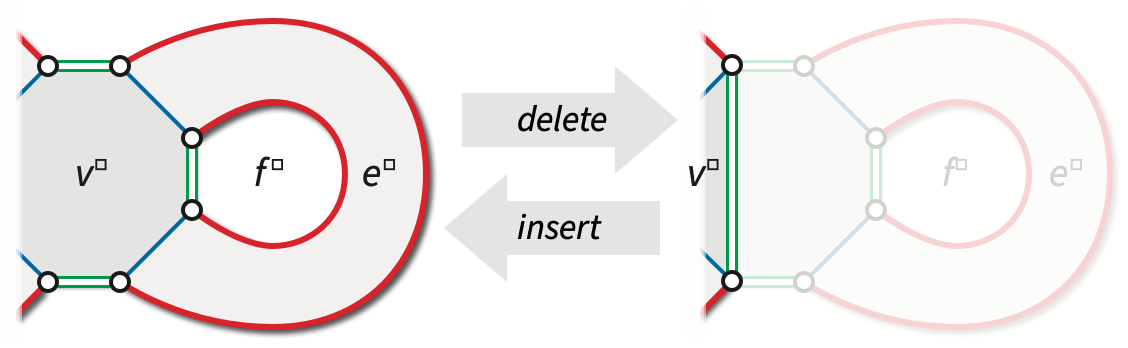
Duality generalizes naturally from planar maps to surface maps. Two surface maps \(\Sigma\) and \(\Sigma^*\) of the same underlying surface are duals if (up to homeomorphism) each face of \(\Sigma\) contains exactly one vertex of \(\Sigma^*\), each face of \(\Sigma^*\) contains exactly one vertex of \(\Sigma\), and each edge of \(\Sigma\) crosses exactly one edge of \(\Sigma^*\).
Just as in the planar setting, the dual of a rotation system \(\Sigma = (D, \textsf{rev}, \textsf{succ})\) is obtained by replacing the successor permutation \(\textsf{succ}\) with \(\textsf{succ}^* := \textsf{rev}(\textsf{succ})\); that is, \(\Sigma^* = (D, \textsf{rev}, \textsf{rev}(\textsf{succ}))\). Thus, the darts in any orientable surface map \(\Sigma\) are dual to (or more formally, are) the darts in the dual map \(\Sigma^*\).
Duality for reflection systems is similarly straightforward. Suppose \(\Xi = (\Phi, a, b, c)\) is the reflection system for a surface map \(\Sigma\); exchanging the involutions \(a\) and \(c\), gives us the dual reflection system \(\Xi^* = (\Phi, c, b, a)\), which is the reflection system of its dual map \(\Sigma^*\). (As a mnemonic device, we could refer to the vertices, edges, and faces of the dual map \(\Sigma^*\) as areas, borders, and centroids, respectively.) In this representation, darts in a surface map are dual to (or more formally, are) sides in its dual map, rather than darts.
For orientable surface maps, we have exactly the same correspondences between features in primal and dual rotation systems as we do for planar maps.
| Primal \(\Sigma\) | Dual \(\Sigma^*\) | Primal \(\Sigma\) | Dual \(\Sigma^*\) |
|---|---|---|---|
| vertex \(v\) | face \(v^*\) | \(\textsf{head}(d)\) | \(\textsf{left}(d^*)\) |
| dart \(d\) | dart \(d^*\) | \(\textsf{tail}(d)\) | \(\textsf{right}(d^*)\) |
| edge \(e\) | edge \(e^*\) | \(\textsf{left}(d)\) | \(\textsf{head}(d^*)\) |
| face \(f\) | vertex \(f^*\) | \(\textsf{right}(d)\) | \(\textsf{tail}(d^*)\) |
| \(\textsf{succ}\) | \(\textsf{rev}\circ\textsf{succ}\) | clockwise | counterclockwise |
| \(\textsf{rev}\) | \(\textsf{rev}\) |
There is a similar but slightly more complex correspondence between primal and dual reflection systems. In particular, the dual of a directed map (where every edge has a preferred “head” vertex) on a non-orientable surface is not another directed graph, but rather an sided map (where every edge has a preferred face).
| Primal \(\Sigma\) | Dual \(\Sigma^*\) | Primal \(\Sigma\) | Dual \(\Sigma^*\) |
|---|---|---|---|
| vertex \(v\) | face \(v^*\) | \(a\) | \(c\) |
| blade \(\phi\) | blade \(\phi^*\) | \(b\) | \(b\) |
| dart \(d\) | side \(d^*\) | \(c\) | \(a\) |
| side \(\sigma\) | dart \(\sigma^*\) | \(\textsf{vert}(\phi)\) | \(\textsf{face}(\phi^*)\) |
| edge \(e\) | edge \(e^*\) | \(\textsf{face}(\phi)\) | \(\textsf{vert}(\phi^*)\) |
| face \(f\) | vertex \(f^*\) |
Recall that a loop in a graph is an edge that is incident to only one vertex, and a bridge is an edge whose deletion disconnects the graph. An isthmus in a surface map is an edge that is incident to only one face. As in planar maps, every bridge in a surface map is also an isthmus. The Jordan curve theorem implies that every isthmus in a planar map is also a bridge, but because the Jordan curve theorem does not extend to maps on other surfaces, an an isthmus in a surface map is not necessarily a bridge. Moreover, unlike in planar graphs, the same edge in a surface map can be both a loop and an isthmus.
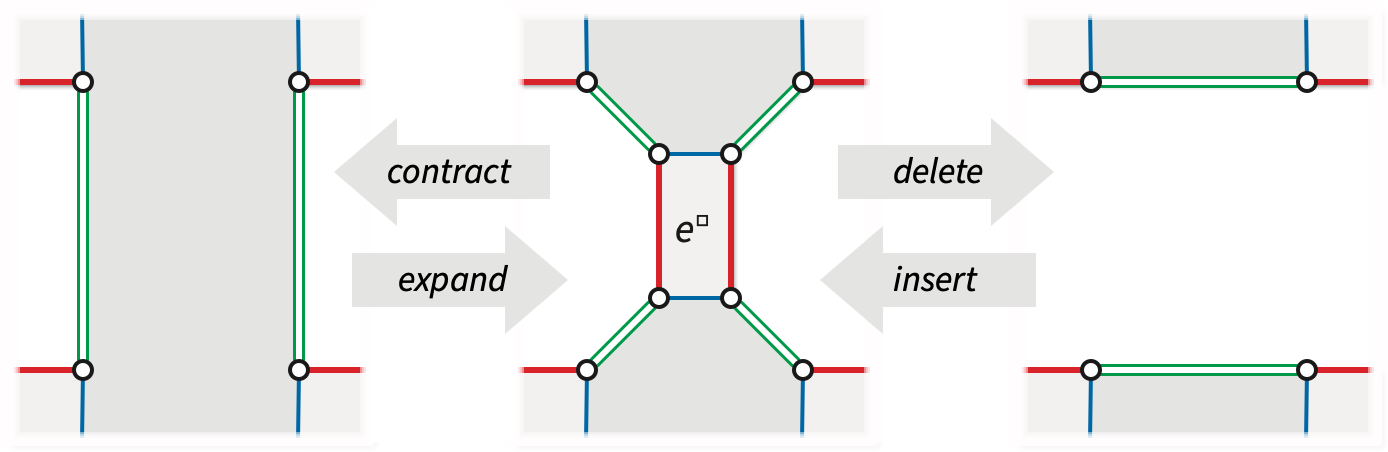
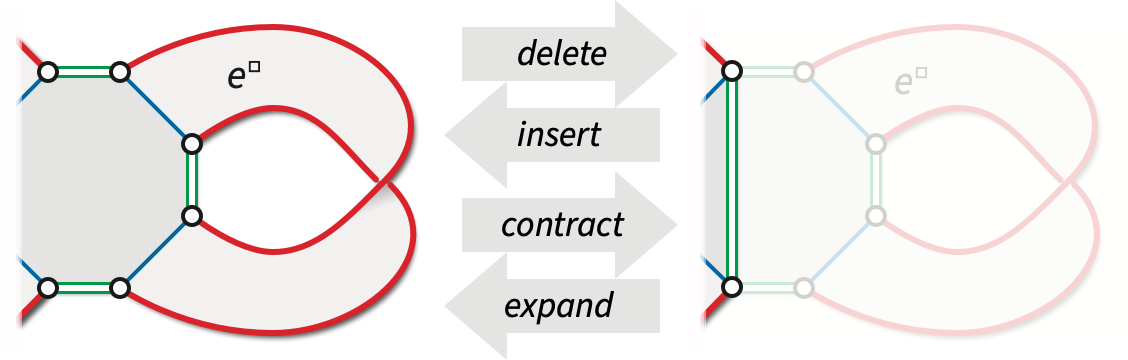
Let \(\Sigma = (V, E, F)\) be an arbitrary surface map. Deleting any edge \(e\) that is not an isthmus yields a simpler map \(\Sigma\setminus e\) of the same surface with the same vertices, one less edge, and with the two faces on either side of \(e\) replaces with their union. Similarly, contracting any edge \(e\) that is not a loop yields a simpler map \(\Sigma / e\) of the same surface with the endpoints of \(e\) merged into a single vertex, one less edge, and the same number of faces.
Contraction and deletion modify the rotation system of an orientable surface map exactly as they do in planar maps: \[ (\textsf{succ}\setminus e)(d) = \begin{cases} \textsf{succ}(\textsf{succ}(\textsf{succ}(d))) \hphantom{^{**}} & \text{if $\textsf{succ}(d) \in e$ and $\textsf{succ}(\textsf{succ}(d)) \in e$,}\\ \textsf{succ}(\textsf{succ}(d)) & \text{if $\textsf{succ}(d) \in e$,}\\ \textsf{succ}(d) & \text{otherwise.} \end{cases} \] \[ (\textsf{succ} \mathbin/ e)(d) = \begin{cases} \textsf{succ}(\textsf{succ}^*(\textsf{succ}^*(d))) & \text{if $\textsf{succ}(d) \in e$ and $\textsf{succ}^*(\textsf{succ}(d)) \in e$,}\\ \textsf{succ}(\textsf{succ}^*(d)) & \text{if $\textsf{succ}(d) \in e$,}\\ \textsf{succ}(d) & \text{otherwise.} \end{cases} \] The first deletion case occurs when the deleted edge is an empty loop; the first contraction case occurs when one endpoint of the contracted edge is a leaf (has degree \(1\)).
Deletion and contraction can be similarly implemented in reflection systems, even in non-orientable maps. If we equate \(e\) with the corresponding set of four flags in \(\Phi\), then the reflection systems \(\Xi\setminus e = (\Phi\setminus e, a, b\setminus e, c)\) and \(\Xi\mathbin/ e = (\Phi\setminus e, a, b\mathbin/ e, c)\), which respectively represent the maps \(\Sigma\setminus e\) and \(\Sigma\mathbin/ e\), can be defined as follows, for all \(\phi \in \Phi\setminus e\): \[ (b\setminus e)(\phi) := \begin{cases} \mathit{b c b c b}(\phi)\quad{} & \text{if~ $b(\phi) \in e$ ~and~ $\mathit{b c b}(\phi) \in e$} \\ \mathit{b c b}(\phi) & \text{if~ $b(\phi) \in e$} \\ b(\phi) & \text{otherwise} \end{cases} \] \[ (b\mathbin/ e)(\phi) := \begin{cases} \mathit{babab}(\phi)\quad{} & \text{if~ $b(\phi) \in e$ ~and~ $\mathit{bab}(\phi) \in e$} \\ \mathit{bab}(\phi) & \text{if~ $b(\phi) \in e$} \\ b(\phi) & \text{otherwise} \end{cases} \] Again, the complicated first cases correspond to the only edge incident to a vertex or an edge. We emphasize the involutions \(a\) and \(c\) from the original reflection system \(\Xi\) appear verbatim (except for their smaller domains) in \(\Xi\setminus e\) and \(\Xi\mathbin/ e\).
Lewis Carroll. Sylvie and Bruno Concluded. Illustrated by Henry Furniss. Macmillan and Co., 1893.
Sóstenes Lins. Graph-encoded maps. J. Comb. Theory Ser. B 32:171–181, 1982.

This construction breaks down when \(D = \varnothing\); in this case, the space \(\mathcal{S}(\Pi)\) is the sphere and \(\Sigma(\Pi)\) is the trivial map with one vertex, one face, and no edges.↩︎
The term “reflection system” is non-standard, but I think it’s both sufficiently evocative and sufficiently similar to “rotation system” to justify its use. Reflection systems are also called graph-encoded maps or graph-encoded manifolds or gems (Lins 1983), but the most common term seems to be “combinatorial map” (or just “map”). Yeah.↩︎