Surface Classification

In this lecture, we will prove that up to homeomorphism, surfaces are uniquely identified by two pieces of data: their genus and their orientability.

The genus of a surface $\mathcal{S}$ is the maximum number of simple disjoint cycles that can be deleted without disconnecting the surface.
A surface $\mathcal{S}$ is orientable if it does not contain a subspace homeomorphic to a Möbius band.

A difficult theorem of Kerékjártó (1923) and Rado (1925) states that every compact 2-manifold is the underlying surface of some map.¹ In light of this result, it suffices to consider an arbitrary surface map $\Sigma$, represented by a reflection system, and argue that the underlying surface of $\Sigma$ is determined by its genus and orientability. By assumption all surface maps are connected.

For any vertex $v$, edge $e$, or face $f$ of $\Sigma$, let $v^\square$, $e^\square$, or $f^\square$ denote the corresponding face of the band decomposition $\Sigma^\square$.

Tree-Cotree Decompositions and Systems of Loops

A tree-cotree decomposition of a surface map $\Sigma$ is a partition of the edges $E = T\sqcup L\sqcup C$, where $T$ is a spanning tree of $\Sigma$, $C^*$ is a spanning tree of the dual map $\Sigma^*$, and $L = E\setminus (C\cup T)$ is the set of leftover edges.

Because $\Sigma$ is connected, $\Sigma$ has a spanning tree $T$, and we can contract all edges in $T$ to obtain a single-vertex map $\Sigma \mathbin/ T$. The dual map $(\Sigma \mathbin/ T)^*$ is also connected, so it has a spanning tree $C$; we can delete the corresponding primal edges $C^*$ to obtain a map $\Sigma \mathbin/ T \setminus C$ that has one vertex, one face, and zero or more edges. Thus, every surface map has a tree-cotree decomposition.

We call any map with a single vertex and a single face a system of loops. Trivially, every edge in a system of loops is both a loop (incident to only one vertex) and an isthmus (incident to only one face). Because contraction and deletion do not change the underlying surface of a map, the Kerékjártó-Rado theorem implies that every surface supports a system of loops. Thus, for purposes of proving the surface classification theorem, we can assume without loss of generality that the original map $\Sigma$ is a system of loops.

For any edge $e$ in a system of loops, the union $e^\square \cup v^\square$ is either a Möbius band or an annulus. If $e^\square \cup v^\square$ is an Möbius band, we call $e$ a one-sided loop; otherwise, $e$ is a two-sided loop.

Handles

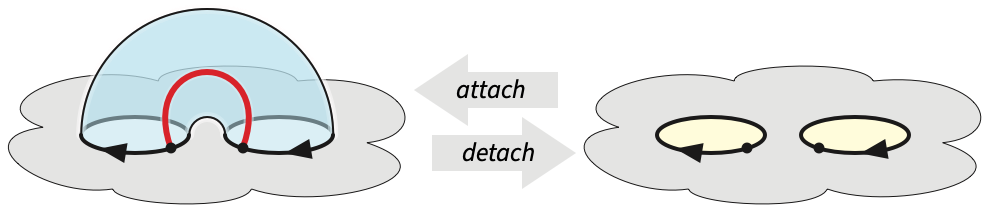
A handle in a surface $\mathcal{S}$ is an annulus $A$ whose complement $\mathcal{S}\setminus A$ is connected. The Jordan curve theorem implies that the sphere has no handles, but this theorem does not extend to other surfaces. To detach the handle, we delete it from $\mathcal{S}$ and glue disks to the two resulting boundary circles, as shown in the figure below.

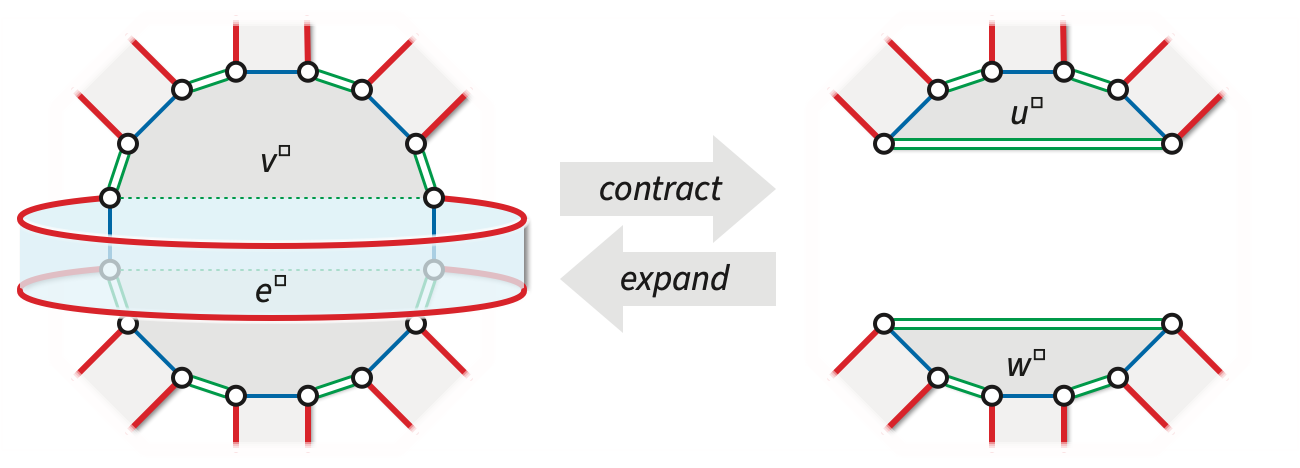
Now suppose our system of loops $\Sigma$ is orientable, or equivalently, that every loop in $\Sigma$ is two-sided. Let $e$ be any loop in $\Sigma$, and let $v$ be its only vertex. Then the band decomposition $\Sigma^\square$ contains a handle $H_e$, composed of $e^\square$ and the rectangle in $v^\square$ connecting the four vertices of $e^\square$; see Figure 2 below.

The two endpoints of $e$ cannot be adjacent around $v$, because then $e$ would be the boundary of an empty loop on one side and another face on the other, contradicting the facet that $\Sigma$ has only one face.

Normally, we are not allowed to contract loops, but for the sake of argument, consider the map $\Sigma \mathbin/ e$ obtained by contracting $e$ using the usual formula for contraction in a reflection system. If $(\Phi, a, b, c)$ is a reflection system for $\Sigma$, then $(\Phi\setminus e, a, b\mathbin/ e, c)$ is a reflection system for $\Sigma \mathbin/ e$, where for any dart $\phi \in \Phi\setminus e$, \[ (b\mathbin/ e)(\phi) := \begin{cases} \mathit{b a b a b}(\phi)\quad{} & \text{if~ $b(\phi) \in e$ ~and~ $\mathit{b c b}(\phi) \in e$} \\ \mathit{b a b}(\phi) & \text{if~ $b(\phi) \in e$} \\ b(\phi) & \text{otherwise} \end{cases} \] Combinatorially, contracting $e$ splits its sole endpoint $v$ of $e$ into two vertices, each incident to the darts that enter $v$ from one side or the other of $e$. (This counterintuitive behavior is exactly why we normally forbid contracting loops.) Topologically, the contraction detaches the handle $H_e$. The resulting map $\Sigma\mathbin/ e$ has two vertices but still only one face.

Detaching a handle by contracting a two-sided loop.

Symmetrically, because $e$ is also an isthmus, deleting $e$ also detaches a handle in the band decomposition, this time consisting of $e^\square$ and a rectangle inside $f^\square$. The resulting map $\Sigma\setminus e$ has two faces but still only one vertex.

Theorem:: Every orientable surface can be reduced to a sphere by detaching zero or more handles.
Proof:: Let $\Sigma$ be any system of loops on an orientable surface $\mathcal{S}$. If $\Sigma$ has no edges, then $\mathcal{S}$ is the sphere. Otherwise, let $e$ be any loop in $\Sigma$. Contracting $e$ detaches a handle from $\mathcal{S}$ and leaves a map $\Sigma\mathbin/ e$ with two vertices and one face. $\Sigma\mathbin/ e$ must contain an edge $e’$ between its two vertices; otherwise, $\Sigma\mathbin/ e$ would be disconnected and thus have more than one face. The map $\Sigma\mathbin/ e \setminus e’$ is a smaller system of loops. By the inductive hypothesis, the underlying surface of $\Sigma\mathbin/ e \setminus e’$ can be reduced to a sphere by detaching handles. $\qquad\square$.

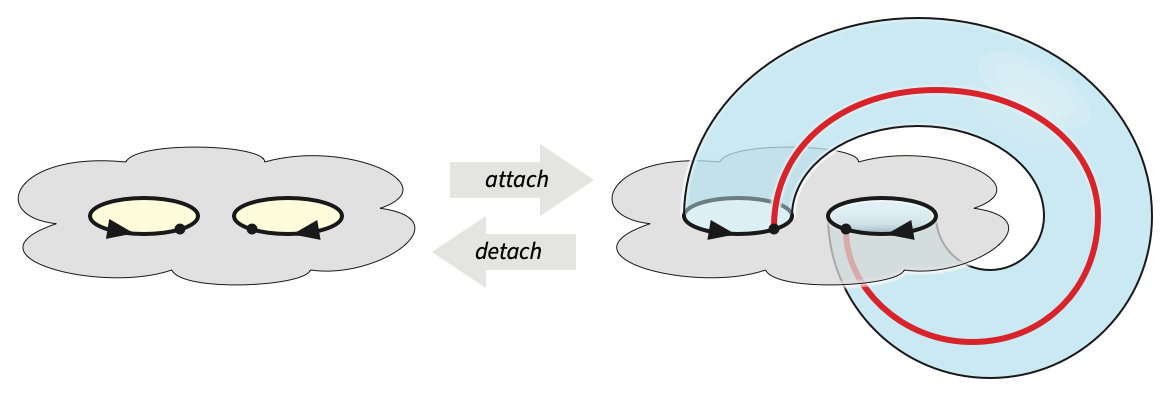
This theorem is more commonly stated in terms of attaching handles. For any integer $g\ge 0$, let $\mathcal{S}(g, 0)$ denote the surface obtained from the sphere by attaching $g$ handles. For example, $\mathcal{S}(0, 0)$ is the sphere and $\mathcal{S}(1, 0)$ is the torus. Up to homeomorphism, it does not matter where or in what order the handles are attached, as long as they are attached in a way that preserves the orientability of the surface (as shown in Figure 1).

Theorem:: Every orientable surface is homeomorphic to $\mathcal{S}(g, 0)$ for some integer $g\ge 0$.

The integer $g$ is called the genus of the surface $\mathcal{S}(g, 0)$, or the genus of any map on that surface.

Twists

A twist in a surface $\mathcal{S}$ is any subspace $M\subset\mathcal{S}$ homeomorphic to a Möbius band. Because $M$ has only one boundary edge, the complement $\mathcal{S}\setminus M$ is always connected. To detach the twist, we delete it from $\mathcal{S}$ and glue a disk to the resulting boundary circle, as shown in the figure below. (Here I am drawing the Möbius band as a self-intersecting surface called a cross-cap, whose boundary is a standard circle, instead of the usual embedding as a twisted paper strip.)

Now suppose our system of loops $\Sigma$ is non-orientable, or equivalently, that $\Sigma$ contains at least one one-sided loop. Let $e$ be any one-sided loop in $\Sigma$. Then the band decomposition $\Sigma^\square$ contains a twist $M_e$, composed of $e^\square$ and the rectangle in $v^\square$ connecting the four vertices of $e^\square$; see Figure 4 below. In this case, the two endpoints of $e$ can be adjacent around $v$.

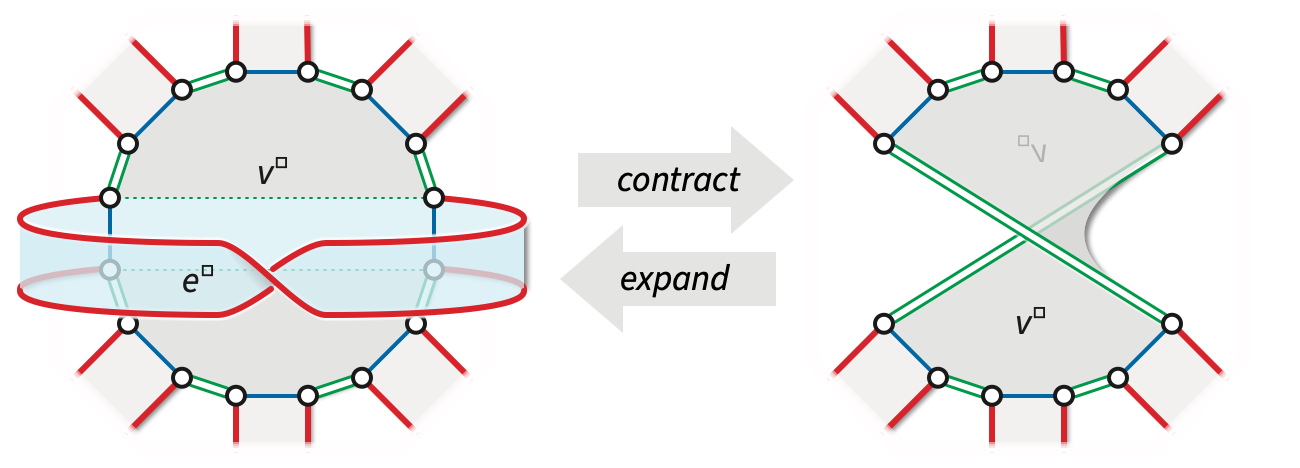
Detaching a handle by contracting a one-sided loop.

Once again, consider the map $\Sigma \setminus e$ obtained by contracting $e$ using the usual formula for contraction in a reflection system. Combinatorially, contracting $e$ reverses the cyclic order of the incoming darts on one side of $e$. (If the darts of $e$ are adjacent around $v$, then all other darts into $v$ are on the same side of $e$, so nothing gets reversed.) Topologically, the contraction detaches the twist $M_e$. The resulting map $\Sigma\mathbin/ e$ is still a system of loops.

Symmetrically, because $e$ is also an isthmus, deleting $e$ also detaches a twist in the band decomposition, this time consisting of $e^\square$ and a rectangle inside $f^\square$. The resulting map $\Sigma\setminus e$ is actually isomorphic (not just homeomorphic!) to $\Sigma\mathbin/ e$.

Theorem:: Every surface can be reduced to a sphere by detaching zero or more twists, and then detaching zero or more handles.

For any integers $g\ge 0$ and $h\ge 0$, let $\mathcal{S}(g, h)$ denote the surface obtained from the sphere by attaching $g$ handles and $h$ twists. Up to homeomorphism, it does not matter where or in what order the handles and twists are attached. In particular, if $h>0$, we can even attach disorienting handles that destroy the orientability of the surface. The surface $\mathcal{S}(g, h)$ is orientable if and only if $h=0$.

Detaching or attaching a disorienting handle.

Theorem:: Every non-orientable surface is homeomorphic to $\mathcal{S}(g, h)$ for some integers $g\ge 0$ and $h > 0$.

Dyck’s Surface

Our classification of surfaces into classes $\mathcal{S}(g, h)$ is not yet complete, because the same non-orientable surface can have multiple classifications, depending on the order in which we contract one-sided loops.

Consider the following example, called Dyck’s surface after its discoverer Walter von Dyck (1888).² Let $\Sigma$ be a system of three one-sided loops $x, y, z$ incident to the unique vertex in the order $x, y, z, x, y, z$. Contracting $x$ gives us an orientable system of loops on the torus $\mathcal{S}(1, 0)$, implying that $|\Sigma| = \mathcal{S}(1, 1)$. On the other hand, contracting edge $y$ yields a non-orientable system of loops on the Klein bottle $\mathcal{S}(0, 2)$, implying that $|\Sigma| = \mathcal{S}(0, 3)$. We conclude that $\mathcal{S}(1, 1)$ and $\mathcal{S}(0, 3)$ are actually the same surface.

A straightforward inductive argument now implies the following more general equivalence, which in turn implies a simpler classification of non-orientable surfaces.

Lemma (Dyck): $\mathcal{S}(g,h) = \mathcal{S}(0,h+2g)$ for all positive integers $g$ and $h$.

Theorem:: Every non-orientable surface is homeomorphic to $\mathcal{S}(0, g)$ for some positive integer $g > 0$.

Again, the integer $g$ is called the genus of the surface $\mathcal{S}(0, g)$, or of any map on that surface.

Canonical Polygonal Schemata

Write this

“Oiler’s” Formula

The Euler characteristic $\chi(\Sigma)$ of a surface map $\Sigma = (V, E, F)$ is the integer $|V|-|E|+|F|$. Euler’s formula states that every planar map has Euler characteristic $2$. The following generalization, first proposed³ by the French mathematician Simon Antoine Jean l’Huillier in 1811, implies that the Euler characteristic is actually an invariant of the underlying surface.

Theorem:: Every map on the surface $\mathcal{S}(g, h)$ has Euler characteristic $2-2g-h$.
Proof:: Contraction and deletion preserve both the underlying surface and the Euler characteristic, so it suffices to consider a system of loops $\Sigma$. There are three cases to consider:; The trivial map (with one vertex, one face, and no edges) on the sphere $\mathcal{S}(0,0)$ clearly has Euler characteristic $2$.; Suppose $\Sigma$ is orientable but not planar. Let $e$ be any loop in $\Sigma$, and let $e’$ be any edge between the two vertices of $\Sigma\mathbin/ e$. The system of loops $\Sigma\mathbin/ e \setminus e’$ has two fewer loops than $\Sigma$, and therefore has Euler characteristic $\chi(\Sigma) + 2$. It follows by induction that $\chi(\mathcal{S}(g, 0)) = 2-2g$.; Finally, suppose $\Sigma$ is non-orientable. Let $e$ be any one-sided loop in $\Sigma$. The system of loops $\Sigma\mathbin/ e$ has one fewer loops than $\Sigma$, and therefore has Euler characteristic $\chi(\Sigma) + 1$. It follows by induction that $\chi(\mathcal{S}(g, h)) = \chi(\mathcal{S}(g, 0)) - h = 2-2g-h$. $\qquad\square$
Corollary:: Two surface maps lie on the same underlying 2-manifold if and only if (1) they are either both orientable or both non-orientable and (2) their Euler characteristics are equal.
Corollary:: For any tree-cotree decomposition $(T, L, C)$ of any surface map $\Sigma$, we have $|L|= 2 - \chi(\Sigma)$.

The Combinatorial Gauss-Bonnet theorem also immediately generalizes from planar maps to surface maps. Let $\Sigma$ be any surface map. Assign an arbitrary real value $\angle c$ to each corner $c$ of a planar map $\Sigma$, called the exterior angle at $c$. Recall that combinatorial curvature of a face $f$ or a vertex $v$, with respect to this angle assignment, is defined as follows: \[ \kappa(f) := 1 - \sum_{c\in f} \angle c \qquad\qquad \kappa(v) := 1 - \frac{1}{2} \deg(v) + \sum_{c\in v} \angle c \]

The Combinatorial Gauss-Bonnet Theorem:: For any surface map $\Sigma = (V, E, F)$ and for any assignment of angles to the corners of $\Sigma$, we have $\sum_{v \in V} \kappa(v) + \sum_{f \in F} \kappa(f) = \chi(\Sigma)$.
Proof:: We immediately have $\sum_f \kappa(f) = |F| - \sum_c \angle c$ and $\sum_v \kappa(f) = |V| - |E| + \sum_c \angle c$, which implies that $\sum_v \kappa(v) + \sum_f \kappa(f) = |V| - |E| + |F| = \chi(\Sigma)$ by definition. $\qquad\square$.

Die Hauptvermutung

Theorem:: Any two maps on the same surface have a common refinement.

References

Aptly Named Sir

This claim may seem obvious; in fact is was considered obvious until the early 20th century. The same claim is false for 4-dimensional manifolds!↩︎
Dyck may be better known to computer scientists for proposing the Dyck language, which is the language of all properly balanced strings of brackets [ and ]. The Dyck language is also the set of all possible crossing sequence of a closed curve with winding number $0$ around the origin with an arbitrary ray from the origin.↩︎
Actually, l’Huillier only proposed this formula for the special (orientable) case of polyhedra with disjoint prismatic tunnels. The full classification theorem is arguably due to August Möbius (1863), but was not properly formalized until the early 20th century, after the proof of the Jordan Curve Theorem.↩︎