Let’s return to one of the earliest problems we saw this semester: Given two curves in the same surface, decide whether they are homotopic, meaning one can be continuously deformed into the other. Here I’ll describe a linear-time algorithm that slightly improves a classical algorithm of Max Dehn (1911).
To keep things simple, I’ll focus on the following special case: Given a closed curve \(\gamma\) in some surface \(\mathcal{S}\), is \(\gamma\) contractible in \(\mathcal{S}\)? That is, can \(\gamma\) be continuously deformed on the surface \(\mathcal{S}\) to a single point?
This question is obviously trivial in the plane or the sphere, and it turns out to be easy on the projective plane, torus, or Klein bottle, so without loss of generality, I will assume that the underlying surface has negative Euler characteristic \(\chi<0\). Let \(\bar{g} = 2-\chi\) denote the Euler genus of the input surface; recall that the Euler genus is equal to the standard genus if the surface is non-orientable, and twice the standard genus otherwise.
Let \(W\) be a given closed walk through some surface map \(\Sigma\). Like every other surface-map algorithm, we begin by computing an arbitrary tree-cotree decomposition \((T, L, C)\) of \(\Sigma\). We then reduce \(\Sigma\) to a system of \(\bar{g}\) loops \(\Lambda = \Sigma \mathbin / T \setminus C\) by contracting every edge in \(T\) and then deleting every edge in \(C\). simultaneously modifying the closed walk \(W\) as follows:
When we contract edges in \(T\), we simply remove any darts of \(T\) from \(W\). After all edges in \(T\) are contracted, all remaining edges are loops.
Then when we delete edges in \(C\), we replace each dart in \(W\) whose edge is in \(C\) with a walk around the boundary of the unique face of \(\Lambda\), as shown in the figure below.

The reduction takes \(O(n + \ell’) = O(n + \bar{g}\ell)\) time to compute, where \(n\) is the complexity of the input map \(\Sigma\), \(\ell\) is the length of the input walk \(W\) in \(\Sigma\), and \(\ell’\) is the length of the transformed walk \(W’\) in \(\Lambda\). (Later I’ll remove the factor of \(\bar{g}\) by reducing to a slightly different map.)
We have now reached the special case of the homotopy problem that Dehn actually solved in 1911: Given a closed walk in a system of loops, is there a sequence of spur and face moves that reduce it to a trivial walk?
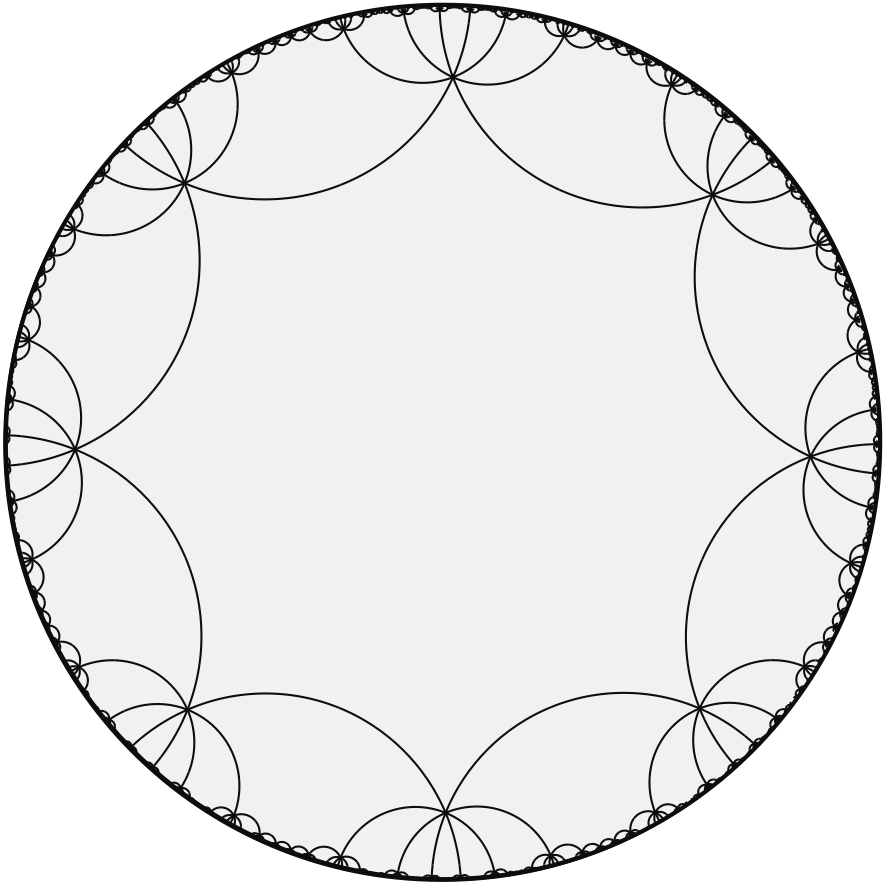
The universal cover \(\tilde\Lambda\) of \(\Lambda\) is an infinite planar map obtained by gluing an infinite lattice of copies of the single face of \(\Lambda\) along corresponding edges. Combinatorially, \(\tilde\Lambda\) is isomorphic to a regular tiling of the hyperbolic plane by regular \(2\bar{g}\)-gons meeting \(2\bar{g}\) at each vertex. For example, if the input map \(\Sigma\) is an orientable map with genus \(2\), and therefore Euler genus \(4\), we reduce \(\Sigma\) to a system of loops \(\Lambda\) containing four loops. The universal cover \(\tilde\Lambda\) of \(\Lambda\) is an \(8\)-regular hyperbolic tiling by octagons.
Formally, a covering map is a continuous surjection \(\pi\colon X’\to X\) between topological spaces, such that each point \(x\in X\) lies in an open neighborhood \(U\subset X\) whose preimage \(\pi^{-1}(U)\) is the disjoint union of open sets \(\bigsqcup_{i\in I} U_i\), where the restriction of \(\pi\) to each set \(U_i\) is a homeomorphism to \(U\). Space \(X'\) is called a covering space of \(X\) if there is a covering map from \(X'\) to \(X\). By convention, covering spaces are assumed to be connected.
Covering maps can also be formulated combinatorially as follows. A map-covering map is a surjective function \(\pi\colon \Sigma’\to\Sigma\) between surface maps that sends vertices to vertices, darts to darts, and faces to faces, and that preserves degrees of vertices and faces. For example, if the maps \(\Sigma’\) and \(\Sigma\) are represented rotation systems \((D’, \textsf{rev}’, \textsf{succ}’)\) and \((D, \textsf{rev}, \textsf{succ})\), a covering map is a function \(\pi\colon D’\to D\) such that \(\textsf{rev}\circ \pi = \pi\circ \textsf{rev}’\) and \(\textsf{succ}\circ \pi = \pi\circ \textsf{succ}’\), and \(\pi\) sends every orbit of \(\textsf{succ}’\) or \(\textsf{rev}’(\textsf{succ})’\) bijectively to an orbit of \(\textsf{succ}\) or \(\textsf{rev}(\textsf{succ})\), respectively. There is a similar combinatorial formulation for reflection systems.
A lift of any vertex \(v\) of \(\Sigma\) to a covering space \(\Sigma’\) is a vertex \(v’\) of \(\Sigma’\) such that \(\pi(v’)=v\). Lifts of darts, edges, and faces are defined similarly. Locally, it is impossible to distinguish between a feature of \(\Sigma\) and any of its lifts in \(\Sigma’\).
The universal cover of a space \(X\) is the unique (connected) covering space \(\tilde{X}\) that is simply connected, meaning all closed curves are contractible. The universal cover \(\tilde{X}\) is also the “largest” (connected) covering space of \(X\), meaning \(\tilde{X}\) is a covering space of every (connected) covering space of \(X\). For almost all surfaces, the universal cover is homeomorphic to the plane. (The only exceptions are the sphere, which is its own universal cover, and the projective plane, whose universal cover is the sphere.) Similarly, universal cover of any surface map \(\Sigma\) is a spherical map if \(\Sigma\) lies on the sphere or the projective plane, and an infinite planar map otherwise.
First, let \(\tilde{W}\) be any closed walk in \(\tilde\Sigma\), and let \(W = \pi(\tilde{W})\). Because \(\tilde\Sigma\) is simply connected, \(\tilde{W}\) must be contractible. Consider any sequence of spur moves and face moves \(\tilde{W}_0 \to \tilde{W}_1 \to \tilde{W}_2 \to \cdots \to \tilde{W}_N\) that reduces \(\tilde{W} = \tilde{W}_0\) to a trivial closed walk \(\tilde{W}_N\). For each index \(i\), let \(W_i = \pi(\tilde{W}_i)\). Then \(W_0 \to W_1 \to W_2 \to \cdots \to W_N\) is also a sequence of spur moves and face moves that reduces \(W = W_0\) to a trivial walk \(W_N\). Specifically, if \(\tilde{W}_{i-1}\to \tilde{W}_i\) is a spur move on some edge \(\tilde{e}\), then \({W}_{i-1}\to {W}_i\) is a spur move on the edge \(\pi(\tilde{e})\), and if \(\tilde{W}_{i-1}\to \tilde{W}_i\) is a face move on some edge \(\tilde{f}\), then \({W}_{i-1}\to {W}_i\) is a face move on the edge \(\pi(\tilde{f})\). We conclude that \(W\) is contractible.
Conversely, let \(W\) be any closed walk in \(\Sigma\). Formally, \(W\) is an alternating sequence \(v_0, d_1, v_1, d_2, \dots, d_\ell, v_\ell\) of vertices and darts, where \(v_\ell = v_0\) and for each index \(i\), we have \(v_{i-1} = \textsf{tail}(d_i)\) and \(v_i = \textsf{head}(d_i)\). We can iteratively lift \(W\) to a (not necessarily closed) walk \(\tilde{W}\) as follows. First, let \(\tilde{v}_0\) be any lift of \(v_0\), and then for each index \(i>0\), let \(\tilde{d}_i\) be the unique lift of \(d_i\) whose tail is \(\tilde{v}_{i-1}\), and let \(\tilde{v}_i = \textsf{head}(\tilde{d}_i)\).
Now suppose \(W\) is contractible. Then there is a sequence \(W_0 \to W_1 \to W_2 \to \cdots \to W_N\) of spur and face moves transforming some trivial walk \(W_0\) into \(W_N = W\). (Yes, we are expanding here rather than contracting.) Fix an arbitrary lift \(\tilde{W}_0\) of \(W_0\). Then for each index \(j\), let \(\tilde{W}_j\) be the closed walk in \(\tilde{X}\) obtained from \(\tilde{W}_{j-1}\) by lifting the move \(W_{j-1}\to W_j\). Specifically, if \(W_{j-1}\to W_j\) inserts a spur \(v_i\mathord\to w\mathord\to v_i\) into \(W_{j-1}\) at its \(i\)th vertex \(v_i\), then \(\tilde{W}_j\) is obtained by inserting a spur \(\tilde{v}_i\mathord\to \tilde{w}\mathord\to \tilde{v}_i\) into \(\tilde{W}_{j-1}\) at its \(i\)th vertex \(\tilde{v}_i\), where \(\tilde{v}_i\mathord\to \tilde{w}\) is the unique lift of dart \(v_i\mathord\to w\) whose tail is \(\tilde{v}_i\). Face moves can be lifted similarly. By induction, each of the resulting walks \(\tilde{W}_j\) is closed, and therefore the final walk \(\tilde{W}_N\) is a closed walk such that \(\pi(\tilde{W}_N) = W\). \(\qquad\square\)
With this lemma in hand, we can now phrase the contractibility problem in the form that Dehn’ considered it. Given a closed walk \(W\) in some system of loops \(\Lambda\), is \(W\) the projection of a closed walk in the universal cover \(\tilde\Lambda\)?
We use a version of the combinatorial Gauss-Bonnet theorem for surfaces with boundary (some faces marked as missing). Here curvature is defined as \[ \kappa(f) = 1 - \sum_{c\in f}\angle c \qquad \kappa(v) = 1 - \frac{1}{2} \deg(v) + \sum_{c\in v}\angle c \] where \(\deg(v)\) is the number of darts incident to \(v\), not the number of corners. Then as usual we have \(\sum_v \kappa(v) + \sum_f \kappa(f) = \chi\). In our application, we will always set \(\angle c = 1/4\), so \[ \kappa(f) = 1 - \frac{1}{4}\deg(f) \qquad \kappa(v) = 1 - \frac{1}{2}\deg(v) + \frac{1}{4}\deg_2(v) \] where \(\deg_2(v)\) is the number of corners incident to \(v\).
Call a boundary vertex of \(\Delta\) convex if it is incident to exactly one face of \(\Delta\). Every convex boundary vertex has degree \(2\) in \(\Delta\) and therefore has curvature \(1/4\); all other vertices of \(\Delta\) have curvature at most \(0\).
The combinatorial Gauss-Bonnet theorem implies that \(\sum_v\kappa(v) + \sum_f\kappa(f) = 1\), which implies that \[ \left(1-\frac{\bar{g}}{2}\right) |F| + \frac{1}{4} |V_+| \ge 1 ~\implies~ |V_+| \ge (2\bar{g}-4) |F| + 4 \] where \(V_+\) is the set of convex vertices. It follows that some face \(f\) is incident to \(2\bar{g}-3\) convex boundary vertices. These must be consecutive around the boundary of \(f\). We conclude that \(f\) has \(2\bar{g}-2\) consecutive edges on the boundary of \(\Delta\). In fact, there must be at least two such face, unless \(\Delta\) consists of a single face.
Now suppose \(\tilde{W}\) is a non-simple closed walk in \(\tilde\Lambda\). If \(\tilde{W}\) contains a sure, we are done, so assume otherwise. Let \(\tilde{x}\) be the first vertex to appear more than once along \(\tilde{W}\), and let \(\tilde{X}\) be subwalk of \(\tilde{W}\) from the first occurrence of \(\tilde{x}\) to the second. If \(\tilde{X}\) is the boundary of a single face \(f\), then \(\tilde{W}\) contains \(2\bar{g}\) consecutive boundary edges of \(f\). Otherwise, there are at least two faces \(f\) such that \(\tilde{X}\) contains at least \(2\bar{g}-2\) consecutive edges on the boundary of \(f\). These two subpaths are disjoint, so at most one of them contains \(x\), so at least one of them is a subpath of \(\tilde{W}\). \(\qquad\square\)
Projection back to the system of loops immediately gives us the following corollary.
Finally, Dehn’s algorithm uses a simple greedy improvement strategy: Repeatedly remove spurs (using spur moves) and long boundary subpaths (using face moves) from \(W’\) until no more remain, and then return \(\textsf{true}\) if and only if the remaining walk is trivial. Correctness follows immediately from Dehn’s lemma.
To find long boundary subpaths efficiently, we assign a unique label to each dart and represent \(W\) as a (circular) string of dart labels, sorted in a circular linked list. Then we slide a window of length \(2\bar{g}-2\) over the string, checking each of the \(O(\bar{g})\) possible long boundary subpaths at each position. Using brute force string comparisons, this check takes \(O(\bar{g}^2)\) time per position. We can improve this to \(O(1)\) time per position by building a DFA that matches all long boundary subpaths; building this DFA adds \(O(\bar{g}^2)\) time to preprocessing.
Whenever we find a long boundary subpath, we replace it with its complement (of length \(2\)) and move the window back \(2\bar{g}\) steps; we charge both the deletion and the time to find the long boundary subpath to the decrease in string length. Similarly, whenever we notice a spur, we can remove it in \(O(1)\) time. The algorithm ends after \(O(\ell’)\) iterations.
Thus, the overall running time of Dehn’s algorithm, starting with an arbitrary surface map \(\Sigma\) with complexity \(n\) and Euler genus \(\bar{g}\), is \(O(n + \bar{g}^2 + \bar{g}\ell)\).
To remove the dependence on \(\bar{g}\) in the running time, we reduce to a different elementary map called a system of quads.
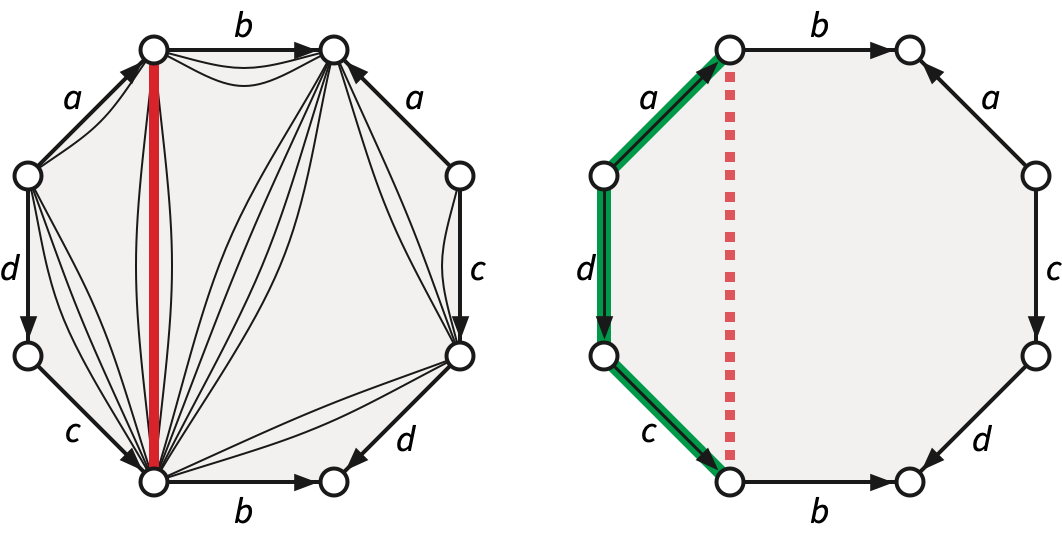
For any surface map \(\Sigma = (V, E, F)\), the radial map \(\Sigma^\diamond = (V^\diamond, E^\diamond, F^\diamond)\) is defined as follows:
A system of quads is the radial map of a system of loops: \(Q = \Lambda^\diamond\). This map has exactly \(2\) vertices, \(2\bar{g}\) edges, and \(\bar{g}\) quadrilateral faces.
We can reduce an arbitrary closed walk \(W\) in an arbitrary map \(\Sigma\) to a homotopic closed walk \(W’\) in a system of quads \(Q\) by modifying our earlier reduction to a system of loops. Fix an arbitrary tree-cotree decomposition \((T, L, C)\), and contract the edges in the spanning tree \(T\). Let \(v\) and \(f\) respectively denote the only vertex and the only face of the system of loops \(\Lambda = \Sigma\setminus T \mathbin/ C\). Each edge \(e\) of \(\Sigma\setminus T\) can be considered (or perturbed into) a path through \(f\) from one corner to another. We replace each such edge with the corresponding path of length \(2\) in \(Q = \Lambda^\diamond\), from \(v\) to \(f^*\) to \(v\). The resulting walk \(W’\) in \(Q\) has length at most \(2\ell\), and the reduction requires \(O(n+\ell)\) time.
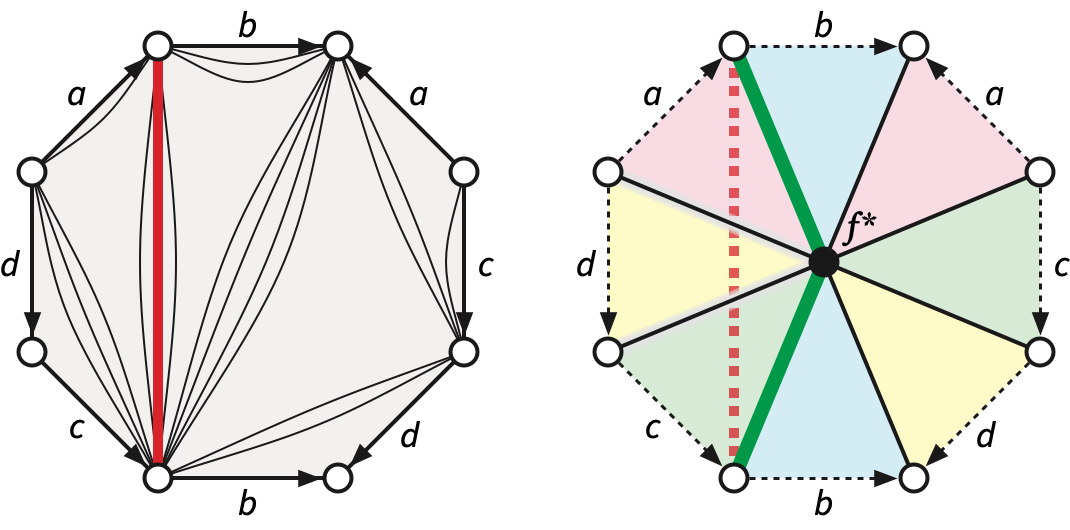
The universal cover of \(Q\) is a hyperbolic tiling by squares meeting \(2\bar{g}\) at each vertex. Our earlier arguments imply that \(W’\) (and therefore \(W\)) is contractible if and only if \(W’\) is the projection of a closed walk in the universal cover \(\tilde{Q}\).
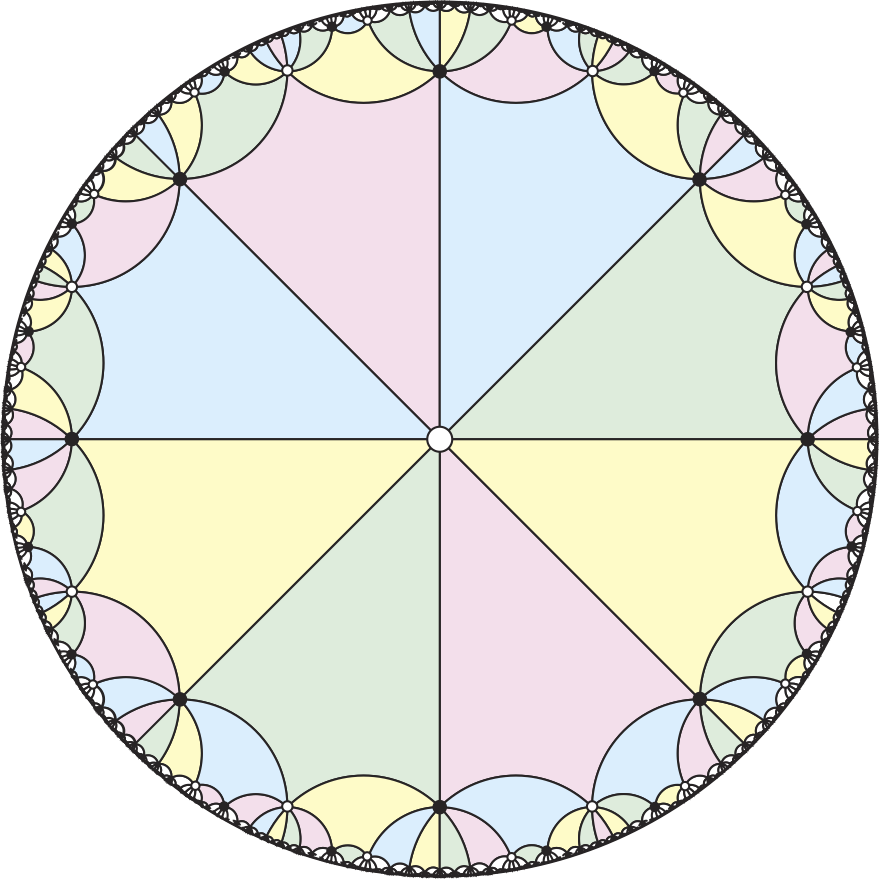
Dehn’s lemma still applies to the infinite hyperbolic tiling \(\tilde{Q}\)—Every closed walk in \(\tilde{Q}\) contains either a spur of a subpath that covers all but two edges of some face. But now the complement of a “long” boundary subpath also has length \(2\); a single face move does not necessarily decrease the length of the walk. We need to find larger moves that are still simple enough to find and execute quickly, but that are guaranteed to shrink any closed walk.
To make this easier, we encode the walk \(W’\) as a turn sequence. The turn of any subwalk \(u\mathord\to v\mathord\to w\) of \(W\) is the number of corners at the middle vertex \(v\) to the left of that subpath, modulo \(\bar{g}\). Thus, for example, a spur is any subpath of \(W\) with turn \(0\). The regularity of the tiling \(\tilde{Q}\) implies that the contractibility of any closed walk depends only on its (cyclic) turn sequence. Moreover, we can easily compute the turn sequence of any walk in time proportional to its length.
A right bracket is any subpath whose turn sequence consists of \(1\), followed by zero or more \(2\)s, followed by \(1\). A left bracket is any subpath whose turn sequence has the form \(-1, -2, \dots, -2, -1\), for any number of \(-2\)s. (In the interest of readability, from now on I will indicate negation with a bar instead of a minus sign; for example, \(\bar{2} = -2\).)
Bracket figure
The previous lemma implies that we can reduce any nontrivial contractible closed walk in \(Q\) either using a spur move or by “sliding” a bracket. Both of these moves can be performed entirely by modifying the turn sequence. For example, removing a spur preceded by turn \(x\) and followed by turn \(y\) leaves a single turn with value \(x+y\). (All turn arithmetic is implicitly performed modulo \(\bar{g}\).) \[ \begin{aligned} x, ~ 0, ~ y &\leadsto x+y \\ x, ~ 1, ~ 2^k, ~ 1, ~ y &\leadsto x-1, ~ \bar2^k, ~ y-1 \\ x, ~ \bar1, ~ \bar2^k, ~ \bar1, ~ y &\leadsto x+1, ~ 2^k, ~ y+1 \\ \end{aligned} \] Here superscripts represent repetition, not exponentiation.
[[bracket slide figure]]
To make detecting and sliding brackets easier, we actually store and manipulate a run-length encoding of the turn sequence. Instead of recording repeated turns explicitly, we store a sequence of pairs \(((\tau_0, r_0), (\tau_1, r_1), \dots)\) to represent \(r_0\) repetitions of turn \(\tau_0\), followed by \(r_1\) repetitions of \(\tau_1\), and so on. Thus, any bracket turn sequence overlaps at most five runs. (In fact, it suffices to encode only runs of \(2\)s and \(\bar2\)s.)
We now proceed as in Dehn’s classical algorithm. We slide a window of width \(5\) over the run-length-encoded turn sequence; whenever the window contains a spur or a bracket, we modify the runs within the window to perform a spur move or bracket move, and then move the window back five steps. At each window position, we need \(O(1)\) time to detect spurs and brackets, and \(O(1)\) time to perform each spur of bracket move. The algorithm iterates until we have made a complete scan with no reductions, in which case we are done, or at most five runs remain in the run sequence, in which case we can complete the algorithm in O(1) additional time. Standard amortisation arguments imply that the reduction algorithm runs in \(O(\ell)\) time.
Thus, the overall running time of Dehn’s algorithm, starting with an arbitrary surface map \(\Sigma\) with complexity \(n\), is \(O(n + \ell)\), with no hidden dependence on the surface genus.
Max Dehn. Über unendliche diskontinuierliche Gruppen. Math. Ann. 71(1):116–144, 1911.
Max Dehn. Transformation der Kurven auf zweiseitigen Flächen. Math. Ann. 72(3):413–421, 1912.
Tamal K. Dey and Sumanta Guha. Transforming curves on surfaces. J. Comput. Syst. Sci. 58:297–325, 1999.
Jeff Erickson and Kim Whittlesey. Transforming curves on surfaces redux. Proc. 24th Ann. ACM-SIAM Symp. Discrete Algorithms, 1646–1655, 2013.
Francis Lazarus and Julien Rivaud. On the homotopy test on surfaces. Proc. 53rd Ann. IEEE Symp. Found. Comput. Sci., 440–449, 2012. arXiv:1110.4573.