Abstract:
We present a number of new results for the combinatorial game Toads and Frogs. We begin
by presenting a set of simplification rules, which allow us to split positions into
independent components or replace them with easily computable numerical values. Using
these simplication rules, we prove that there are Toads and Frogs positions with arbitrary
numerical values and arbitrarily high temperatures, and that any position in which all the
pieces are contiguous has an integer value that can be computed quickly. We also give a
closed form for the value of any starting position with one frog, and derive some partial
results for two-frog positions. Finally, using a computer implementation of the rules, we
derive new values for a large number of starting positions.
 Update (22 May 2000): Jesse Hull
has proved that Toads and Frogs is NP-hard, using a program that automates simple
induction proofs involving Toads and Frogs positions. Specifically, his program
found the following identity, which by results of Yedwab and Moews is enough to
show NP-hardness:
Update (22 May 2000): Jesse Hull
has proved that Toads and Frogs is NP-hard, using a program that automates simple
induction proofs involving Toads and Frogs positions. Specifically, his program
found the following identity, which by results of Yedwab and Moews is enough to
show NP-hardness:
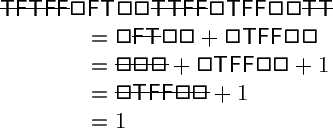
 Publications -
Jeff Erickson
(jeffe@cs.uiuc.edu)
22 May 2000
Publications -
Jeff Erickson
(jeffe@cs.uiuc.edu)
22 May 2000